
【题目】如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=3,BE=![]() ,求半圆和菱形ABFC的面积.
,求半圆和菱形ABFC的面积.

【答案】(1)见解析;(2) ![]() .
.
【解析】
(1)根据对角线相互平分的四边形是平行四边形,证明是平行四边形,再根据邻边相等的平行四边形是菱形即可证明;
(2)设CD=x,连接BD.利用勾股定理构建方程即可解决问题;
(1)证明:∵AB是直径,
∴∠AEB=90°
∴AE⊥BC,
∵AB=AC,
∴BE=CE,
∵AE=EF,
∴四边形ABFC是平行四边形,
∵AC=AB,
∴四边形ABFC是菱形
(2)设CD=x.连接BD.
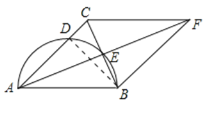
∵AB是直径,
∴∠ADB=∠BDC=90°,
∴AB2-AD2=CB2-CD2,
∴(3+x)2-32=![]() 2-x2,
2-x2,
解得x=2或-5(舍)
∴AB=AC=5,BD=![]()
∴S菱形ABFC=AC×BD=20
∴S半圆=![]() ×π×
×π×![]() π
π


 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】某经销商销售一种成本价为10元/kg的商品,已知销售价不低于成本价,且物价部门规定这种产品的销售价不得高于18元/kg.在销售过程中发现销量y(kg)与售价x(元/kg)之间满足一次函数关系,对应关系如下表所示:
x | 12 | 14 | 15 | 17 |
y | 36 | 32 | 30 | 26 |
⑴求y与x之间的函数关系式,并写出自变量x的取值范围;
⑵若该经销商想使这种商品获得平均每天168元的利润,求售价应定为多少元/kg?
⑶设销售这种商品每天所获得的利润为W元,求W与x之间的函数关系式;并求出该商品销售单价定为多少元时,才能使经销商所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,如果∠ABD=60°,那么∠BAE的度数是( )

A. 40°B. 55°C. 75°D. 80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级学生体育测试成绩情况,随机抽取九年级部分学生的体育测试成绩为样本,按A,B,C,D四个等级进行统计,并将统计结果绘制成如下两幅不完整的统计图,请你结合图中所给信息解答下列问题:
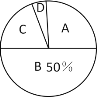
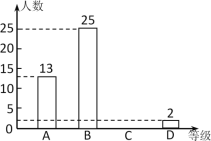
(说明:A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下)
(1)求出A级学生的人数占所抽取总人数的百分比;
(2)求出扇形统计图中C级所在的扇形圆心角的度数;
(3)所抽取学生体育测试成绩的中位数落在 等级内;
(4)若该校九年级共有500名学生,请你估计这次测试中C级和D级的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,BC=6,AC=8,D、E分别是AC、BC上的一点,且DE=6 ,若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为______.
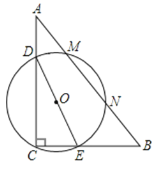
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程mx2﹣2x﹣1=0有两个实数根x1,x2.
(1)求m的取值范围;
(2)当x12+x22=﹣6x1x2时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
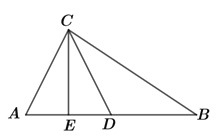
【题目】如图所示.在Rt△ABC中,CD是斜边上的中线,CE是高.已知AB=10cm,DE=2.5cm,则∠BDC=____________度,S△BCD=______cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
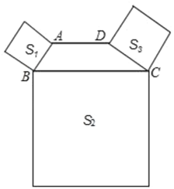
【题目】如图,四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,以AB、BC、DC为边向外作正方形,其面积分别为S1、S2、S3,若S1=2,S3=4,则S2的值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com