
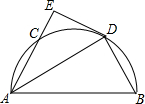
 如图所示,AB为半圆O的直径,C是半圆上一点,AD平分∠CAB交半圆于点D,过点D作DE⊥AC,DE交AC的延长线于点E.
如图所示,AB为半圆O的直径,C是半圆上一点,AD平分∠CAB交半圆于点D,过点D作DE⊥AC,DE交AC的延长线于点E.分析 (1)连接OD,根据等腰三角形的性质和平行线的性质得出∠EDO=90°,即可证得DE是⊙O的切线;
(2)连接BC交OD于F,先证得四边形DECF为矩形,DE=CF=$\sqrt{3}$,∠DFC=90°,进而得出OD⊥BC,根据垂径定理得出BC=2CF=2$\sqrt{3}$,然后根据勾股定理即可求得线段AC的长.
解答 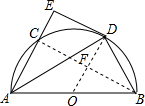 (1)证明:连接OD,
(1)证明:连接OD,
∵OA=OD,
∴∠OAD=∠ADO,
∵AD平分∠CAD,
∴AE∥OD,
∴∠AED+∠EDO=180°,
∵DE⊥AC,
∴∠EDO=90°,
∴DE是⊙O的切线;
(2)连接BC交OD于F,
∵AB为直径,
∴∠ACB=90°,
∵∠AED=∠EDO=90°,
∴四边形DECF为矩形,
∴DE=CF=$\sqrt{3}$,∠DFC=90°,
∴OD⊥BC,
∴BC=2CF=2$\sqrt{3}$,
∵AB=4,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=2.
点评 本题考查了切线的判定,等腰三角形的性质,角平分线的性质,矩形的判定依据垂径定理和勾股定理的应用,作出辅助线构建直角三角形和矩形是解题的关键.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 小明的爸爸每天都到公园锻炼身体,某天小明的爸爸到公园锻炼身体,他行走的路程S(米)与锻炼的时间t(分)之间的函数关系图象如图所示,下列说法:①25分钟时小明的爸爸行走了1200米;②小明的爸爸在公园休息了10分钟;③35-60分钟时行走了800米;④60分钟时小明的爸爸回到了家,其中一定正确的个数是( )
小明的爸爸每天都到公园锻炼身体,某天小明的爸爸到公园锻炼身体,他行走的路程S(米)与锻炼的时间t(分)之间的函数关系图象如图所示,下列说法:①25分钟时小明的爸爸行走了1200米;②小明的爸爸在公园休息了10分钟;③35-60分钟时行走了800米;④60分钟时小明的爸爸回到了家,其中一定正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
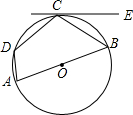 如图,已知四边形ABCD内接于⊙O,AB是⊙O的直径,EC与⊙O相切于点C,∠ECB=35°,则∠D的度数是( )
如图,已知四边形ABCD内接于⊙O,AB是⊙O的直径,EC与⊙O相切于点C,∠ECB=35°,则∠D的度数是( )| A. | 145° | B. | 125° | C. | 90° | D. | 80° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
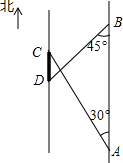 如图,一条南北走向的两岸互相平行.甲、乙二人分别站在河东岸的A、B处观察河西岸某景观建筑物.甲同学测得该建筑物一端C在A的北偏西30°方向,乙同学测得该建筑物另一端D在B的南偏西45°方向上.已知A、B点相距240米,河宽100米,求景观建筑物两端点C、D之间的距离.(结果精确到1米,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
如图,一条南北走向的两岸互相平行.甲、乙二人分别站在河东岸的A、B处观察河西岸某景观建筑物.甲同学测得该建筑物一端C在A的北偏西30°方向,乙同学测得该建筑物另一端D在B的南偏西45°方向上.已知A、B点相距240米,河宽100米,求景观建筑物两端点C、D之间的距离.(结果精确到1米,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com