
 (1)如图1,点C是线段AB上的一点,AB=10,点M,N分别为AC,CB的中点,MN为多少?请说明理由.
(1)如图1,点C是线段AB上的一点,AB=10,点M,N分别为AC,CB的中点,MN为多少?请说明理由.分析 (1)根据线段中点的性质,可得MC,NC的长,根据线段的和差,可得答案;
(2)根据线段的和差,可得(AC+BD)的长,根据线段中点的性质,可得(MC+ND)的长,根据线段的和差,可得答案.
解答 解:(1)MN=5,理由如下:
由点M,N分别为AC,CB的中点,得
MC=$\frac{1}{2}$AC,NC=$\frac{1}{2}$BC.
由线段的和差,得
MN=MC+NC=$\frac{1}{2}$(AC+BC)=$\frac{1}{2}$×10=5;
(2)MN=7,理由如下:
由线段的和差,得
AC+BD=AB-CD=10-4=6.
由点M,N分别为AC,DB的中点,得
MC=$\frac{1}{2}$AC,DN=$\frac{1}{2}$DB.
由线段的和差,得
MN=MC+CD+DN=$\frac{1}{2}$(AC+DB)+CD=$\frac{1}{2}$×6+4=7.
点评 本题考查了两点间的距离,利用线段的和差得出(MC+CD+DN)是解题关键.


科目:初中数学 来源: 题型:解答题
 如图,⊙P的圆心为P(-2,1),半径为2,直线MN过点M(2,3),N(4,1).
如图,⊙P的圆心为P(-2,1),半径为2,直线MN过点M(2,3),N(4,1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一、二象限 | B. | 第一、三象限 | C. | 第二、三象限 | D. | 第二、四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
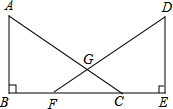 已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=EC.求证:
已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=EC.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC三个顶点的坐标分别为A(2,4),B (1,1),C(4,3).
如图,△ABC三个顶点的坐标分别为A(2,4),B (1,1),C(4,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读与思考:整式乘法与因式分解是方向相反的变形,由(x+p)(x+q)=x2+(p+q)x+pq得,x2+(p+q)x+pq=(x+p)(x+q);利用这个式子可以将某些二次项系数是1的二次三项式分解因式,例如:将式子x2-x-6分解因式.这个式子的常数项-6=2×(-3),一次项系数-1=2+(-3),这个过程可用十字相乘的形式形象地表示:先分解常数项,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数.如图所示.这种分解二次三项式的方法叫“十字相乘法”,请同学们认真观察,分析理解后,解答下列问题.
阅读与思考:整式乘法与因式分解是方向相反的变形,由(x+p)(x+q)=x2+(p+q)x+pq得,x2+(p+q)x+pq=(x+p)(x+q);利用这个式子可以将某些二次项系数是1的二次三项式分解因式,例如:将式子x2-x-6分解因式.这个式子的常数项-6=2×(-3),一次项系数-1=2+(-3),这个过程可用十字相乘的形式形象地表示:先分解常数项,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数.如图所示.这种分解二次三项式的方法叫“十字相乘法”,请同学们认真观察,分析理解后,解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
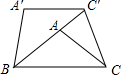 如图,将△ABC绕点B逆时针旋转40°,得到△A′B′C′,若点C′恰好落在边BA的延长线上,且A′C′∥BC,连接CC′,则∠ACC′=30度.
如图,将△ABC绕点B逆时针旋转40°,得到△A′B′C′,若点C′恰好落在边BA的延长线上,且A′C′∥BC,连接CC′,则∠ACC′=30度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com