
如图,在矩形ABCD中,AB=3,BC=4.动点P从点A出发沿AC向终点C运动,同时动点Q从点B出发沿BA向点A运动,到达A点后立刻以原来的速度沿AB返回.点P、Q运动速度均为每秒1个单位长度,当点P到达点C时停止运动,点Q也同时停止.连接PQ,设运动时间为t(t >0)秒.
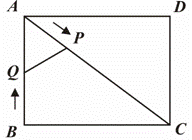

(1)求线段AC的长度;
(2)当点Q从点B向点A运动时(未到达A点),求△APQ的面积S关于t的函数关系式,并写出t的取值范围;
(3)伴随着P、Q两点的运动,线段PQ的垂直平分线为l:
①当l经过点A时,射线QP交AD于点E,求AE的长;
②当l经过点B时,求t的值.
科目:初中数学 来源: 题型:
如图,在直角梯形ABCD中,∠A=90°,∠B=120°,AD=1,AB= ,在底边AB上取点E,在射线DC上取点F,使得∠DEF=120°,当点E是AB的中点时,线段DF的长度是 。
,在底边AB上取点E,在射线DC上取点F,使得∠DEF=120°,当点E是AB的中点时,线段DF的长度是 。

查看答案和解析>>
科目:初中数学 来源: 题型:
有两个全等的等腰直角三角板ABC和EFG其直角边长均为6(如图1所示)叠放在一起,使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点顺时针旋转,旋转角满足0<º<90º,四边形 CHGK是旋转过程中两块三角板的重叠部分(如图2).
CHGK是旋转过程中两块三角板的重叠部分(如图2).
(1)在上述旋转过程中,①BH与CK有怎样的数量关系?②四边形CHGK的面积是否发生变化?并证明你发现的结论.
(2)如图,连接KH,在上述旋转过程中,是否存在某一 位置使△GKH的面积恰好等于△ABC面积的
位置使△GKH的面积恰好等于△ABC面积的
 ?若存在,请求出此时KC的长度;若不存在,请说明理由.
?若存在,请求出此时KC的长度;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
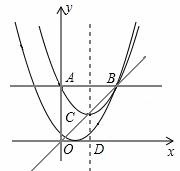
如图,抛物线
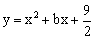 与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第一象限).抛物线的顶点C在直线OB上,对称轴与x轴相交于点
与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第一象限).抛物线的顶点C在直线OB上,对称轴与x轴相交于点 D。平移抛物线,使其经
D。平移抛物线,使其经 过点B、D,则平移后的抛物线的解析式为 。
过点B、D,则平移后的抛物线的解析式为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图(1),Rt△ABC和Rt△EFD中,AC与DE重合,AB=EF=1,∠BAC=∠DEF=90º,∠ ACB=∠EDF=30º,固定△ABC,将△DEF绕点A顺时针旋转,当DF边与AB边重合时,旋转中止。现不考虑旋转开始和结束 时重合的情况,设DE,DF(或它们的延长线)分别交BC(或它的延长线) 于G,H点,如图(2)
时重合的情况,设DE,DF(或它们的延长线)分别交BC(或它的延长线) 于G,H点,如图(2)
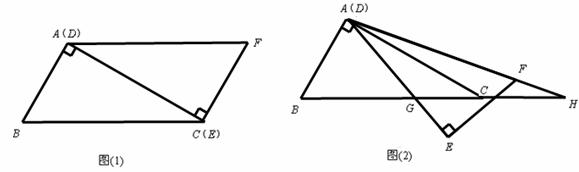
(1)问:始终与△AGC相似的三角形是 ;
(2)设CG=x,BG=y,求y关于x的函数关系式;
(3)问:当x为何值时,△HGA是等腰三角形。
查看答案和解析>>
科目:初中数学 来源: 题型:
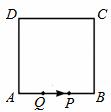
如图,在边长为4的正方形ABCD中,动点P,Q同时从A点出发,沿AB →BC→CD向D点运动,点P的速度是每秒2个单位长度,点Q的速度是每秒1个单位长度,当P运动到D点时,P、Q
→BC→CD向D点运动,点P的速度是每秒2个单位长度,点Q的速度是每秒1个单位长度,当P运动到D点时,P、Q 两点同时停止运动。设P点运动的时间为t,△APQ的面积为S,则S与t的函数关系式是 。
两点同时停止运动。设P点运动的时间为t,△APQ的面积为S,则S与t的函数关系式是 。
查看答案和解析>>
科目:初中数学 来源: 题型:
在△ABC中,P是AB上的动点(P异于A、B),过点P的直线截△ABC,使截得的三角形与△ABC相似,我们不妨称这种直线 为过点P的△ABC的相似线,简记为P(lx)(x为自然数).
为过点P的△ABC的相似线,简记为P(lx)(x为自然数).
(1)如图①,∠A=90°,∠B=∠C,当BP=2PA时,P(l1)、P(l2)都是过点P的△ABC的相似线(其中l1⊥BC,l2∥AC),此外 ,还有 条;
,还有 条;
(2)如图②,∠C=90°,∠B=30°,当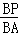
 = 时,P(lx)截得的三角形面积为△A
= 时,P(lx)截得的三角形面积为△A BC面积的
BC面积的
 .
.


查看答案和解析>>
科目:初中数学 来源: 题型:
如图,矩形ABCD中, BC=2,点P是线段BC上一点,连接PA,将线段PA绕点 P逆时针
P逆时针 旋转90°得到线段PE,平移线段PE得到CF,连接EF。问:四边形P
旋转90°得到线段PE,平移线段PE得到CF,连接EF。问:四边形P CFE
CFE 的面积是否有最大值?若有,请求出面积的最大值及此时BP长;若没有,请说明理由。
的面积是否有最大值?若有,请求出面积的最大值及此时BP长;若没有,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
如 图1,已知直线y=kx与抛物线
图1,已知直线y=kx与抛物线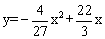
 交于点A(3,6).
交于点A(3,6).


(1)求直线y=kx的解析式和线段OA的长度;
(2)点P为抛物线第一象限内的动点,过点P作直线PM,交x轴于点M(点M、O不重合),交直线OA于点Q,再过点Q作直线PM的垂线,交y轴于点N.试探究:线段 QM与线段QN的长度之比是否为定
QM与线段QN的长度之比是否为定 值?如果是,求出这个定值;如果不是,说明理由;
值?如果是,求出这个定值;如果不是,说明理由;
(3) 如图2,若点B为抛物线上
如图2,若点B为抛物线上 对称轴右侧的点
对称轴右侧的点 ,点E在线段OA上(与点O、A不重合),点D(m,0)是x轴正半轴上的动点,且满足∠BAE=∠BED=∠AOD.继续探究:m在什么范围时,符合条件的E点的个数分别是1个、2个?
,点E在线段OA上(与点O、A不重合),点D(m,0)是x轴正半轴上的动点,且满足∠BAE=∠BED=∠AOD.继续探究:m在什么范围时,符合条件的E点的个数分别是1个、2个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com