
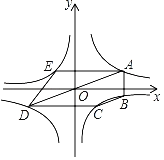
【题目】如图,经过原点O的直线与反比例函数y=![]() (a>0)的图象交于A,D两点(点A在第一象限),点B,C,E在反比例函数y=
(a>0)的图象交于A,D两点(点A在第一象限),点B,C,E在反比例函数y=![]() (b<0)的图象上,AB∥y轴,AE∥CD∥x轴,五边形ABCDE的面积为56,四边形ABCD的面积为32,则a﹣b的值为__,
(b<0)的图象上,AB∥y轴,AE∥CD∥x轴,五边形ABCDE的面积为56,四边形ABCD的面积为32,则a﹣b的值为__,![]() 的值为__.
的值为__.
【答案】24 ﹣![]()
【解析】
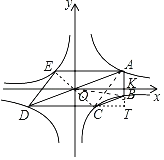
如图,连接AC,OE,OC,OB,延长AB交DC的延长线于T,设AB交x轴于K.求出证明四边形ACDE是平行四边形,推出S△ADE=S△ADC=S五边形ABCDE-S四边形ABCD=56-32=24,推出S△AOE=S△DEO=12,可得![]() a-
a-![]() b=12,推出a-b=24.再证明BC∥AD,证明AD=3BC,推出AT=3BT,再证明AK=3BK即可解决问题.
b=12,推出a-b=24.再证明BC∥AD,证明AD=3BC,推出AT=3BT,再证明AK=3BK即可解决问题.
如图,连接AC,OE,OC,OB,延长AB交DC的延长线于T,设AB交x轴于K.
由题意A,D关于原点对称,
∴A,D的纵坐标的绝对值相等,
∵AE∥CD,
∴E,C的纵坐标的绝对值相等,
∵E,C在反比例函数y=![]() 的图象上,
的图象上,
∴E,C关于原点对称,
∴E,O,C共线,
∵OE=OC,OA=OD,∴四边形ACDE是平行四边形,
∴S△ADE=S△ADC=S五边形ABCDE﹣S四边形ABCD=56﹣32=24,
∴S△AOE=S△DEO=12,
∴![]() a﹣
a﹣![]() b=12,
b=12,
∴a﹣b=24,
∵S△AOC=S△AOB=12,
∴BC∥AD,
∴![]() =
=![]() ,
,
∵S△ACB=32﹣24=8,
∴S△ADC:S△ABC=24:8=1:3,
∴BC:AD=1:3,
∴TB:TA=1:3,设BT=a,则AT=3a,AK=TK=1.5k,BK=0.5k,
∴AK:BK=3:1,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =﹣
=﹣![]() .
.
故答案为24,﹣![]() .
.


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:
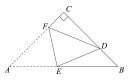
【题目】如图,在△ABC中,AC=BC=4![]() ,∠C=90°,点D在BC上,且CD=3DB,将△ABC折叠,使点A与点D重合,EF为折痕,则tan∠BED的值是_____.
,∠C=90°,点D在BC上,且CD=3DB,将△ABC折叠,使点A与点D重合,EF为折痕,则tan∠BED的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车经营店销售![]() 型,
型,![]() 型两种品牌自行车,今年进货和销售价格如下表:(今年1年内自行车的售价与进价保持不变)
型两种品牌自行车,今年进货和销售价格如下表:(今年1年内自行车的售价与进价保持不变)
|
| |
进货价格(元/辆) | 1000 | 1100 |
销售价格(元/辆) |
| 1500 |
今年经过改造升级后,![]() 型车每辆销售价比去年增加400元.已知
型车每辆销售价比去年增加400元.已知![]() 型车去年1月份销售总额为3.6万元,今年1月份
型车去年1月份销售总额为3.6万元,今年1月份![]() 型车的销售数量与去年1月份相同,而销售总额比去年1月份增加
型车的销售数量与去年1月份相同,而销售总额比去年1月份增加![]() .
.
(1)若设今年1月份的![]() 型自行车售价为
型自行车售价为![]() 元/辆,求
元/辆,求![]() 的值?(用列方程的方法解答)
的值?(用列方程的方法解答)
(2)该店计划8月份再进一批![]() 型和
型和![]() 型自行车共50辆,且
型自行车共50辆,且![]() 型车数量不超过
型车数量不超过![]() 型车数量的2倍,应如何进货才能使这批自行车获利最多?
型车数量的2倍,应如何进货才能使这批自行车获利最多?
(3)该店为吸引客源,准备增购一种进价为500元的![]() 型车,预算用8万元购进这三种车若干辆,其中
型车,预算用8万元购进这三种车若干辆,其中![]() 型与
型与![]() 型的数量之比为
型的数量之比为![]() ,则该店至少可以购进三种车共多少辆?
,则该店至少可以购进三种车共多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过![]() 上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
(1)求证:△ECF∽△GCE;
(2)求证:EG是⊙O的切线;
(3)延长AB交GE的延长线于点M,若tanG=![]() ,AH=
,AH=![]() ,求EM的值.
,求EM的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(基础巩固)
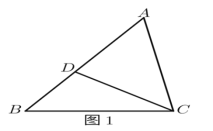
(1)如图1,在△ABC中,D为AB上一点,∠ACD=∠B.求证:AC2=ADAB.
(尝试应用)
(2)如图2,在ABCD中,E为BC上一点,F为CD延长线上一点,∠BFE=∠A.若BF=4,BE=3,求AD的长.
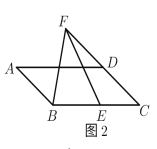
(拓展提高)
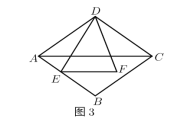
(3)如图3,在菱形ABCD中,E是AB上一点,F是△ABC内一点,EF∥AC,AC=2EF,∠EDF=![]() ∠BAD,AE=2,DF=5,求菱形ABCD的边长.
∠BAD,AE=2,DF=5,求菱形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技的进步和网络资源的丰富,在线学习已成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.
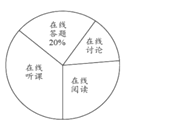
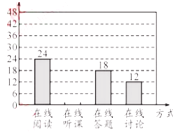
根据图中信息,解答下列问题:
(1)求本次调查的学生总人数,并补全条形统计图;
(2)求扇形统计图中“在线讨论”对应的扇形圆心角的度数;
(3)该校共有学生![]() 人,请你估计该校对在线阅读最感兴趣的学生人数.
人,请你估计该校对在线阅读最感兴趣的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在正方形ABCD中,对角线AC与BD相交于点O,AE,DF分别是∠OAD与∠ODC的平分线,AE的延长线与DF相交于点G,则下列结论:①AG⊥DF;②EF∥AB;③AB=AF;④AB=2EF.其中正确的结论是( )

A.①②B.③④C.①②③D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com