练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

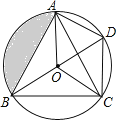
    【题目】如图，O是的内心，BO的延长线和的外接圆相交于D，连结DC、DA、OA、OC，四边形OADC为平行四边形．

    求证：≌．

    若，求阴影部分的面积．

    【答案】（1）证明见解析（2）

    【解析】

    由点O为三角形的内心，得到BO与CO都为角平分线，再由四边形AOCD为平行四边形，得到对边平行且相等，进而利用AAS得到三角形全等；

    由三角形全等得到对应边相等，对应角相等，确定出三角形ABC为等边三角形，可得出内心与外心重合，即，阴影部分面积等于扇形AOB面积减去三角形AOB面积，求出即可．

    是的内心，

    ，，

    ，

    ，

    由，，

    ，

    在和中，

    ，

    ≌；

    由得，，，

    ，

    ，

    是等边三角形，

    是的内心也是外心，

    ，

    设E为BD与AC的交点，BE垂直平分AC，

    在中，，，

    ，

    ，

    ．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图1，CA=CB，CD=CE，∠ACB=∠DCE=α．

    （1）求证：BE=AD；

    （2）当α=90°时，取AD，BE的中点分别为点P、Q，连接CP，CQ，PQ，如图②，判断△CPQ的形状，并加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商场分两次购进A，B两种商品进行销售，两次购进同一种商品的进价相同，具体情况如表所示：

    购进数量件

    购进所需费用元

    A

    B

    第一次

    30

    20

    2200

    第二次

    20

    30

    2800

    求A，B两种商品每件的进价分别是多少元？

    商场决定A种商品以每件30元出售，B种商品以每件100元出售为满足”五一“小长假期间市场需求，需购进A，B两种商品共1000件，且A种商品的数量不少于B种商品数量的4倍，请你求出获利最大的进货方案，此时最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB=90°，D是AB的中点，过点A作AE//BC与过点D作CD的垂线交于点E.

    （1）如图1，若CE交AD于点F，BC=6，∠B=30°，求AE的长；

    （2）如图2，求证AE+CE=BC.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动，活动后，就活动的个主题进行了抽样调查（每位同学只选最关注的一个），根据调查结果绘制了两幅不完整的统计图．根据图中提供的信息，解答下列问题：

    （1）这次调查的学生共有多少名？

    （2）请将条形统计图补充完整，并在扇形统计图中计算出“进取”所对应的圆心角的度数．

    （3）如果要在这个主题中任选两个进行调查，根据（2）中调查结果，用树状图或列表法，求恰好选到学生关注最多的两个主题的概率（将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，△ABC的周长为21cm，AB＝6cm，BC边上中线AD＝5cm，△ACD周长为16cm，则AC的长为__________cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，已知中，点在边上，交边于点，且平分．

    (1)求证：；

    (2)如图2，在边上取点，使，若，，求的长。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD中，∠A = ∠B = 90°,AB边上有一点E,CE,DE分别是∠BCD和∠ADC 的角平分线，如果ABCD的面积是12,CD = 8,那么AB的长度为_____.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在边长为 1 个单位长度的小正方形组成的网格中，点 A、B、C 在小正方形的顶点上．

    （1）在图中画出与△ABC 关于直线 l 成轴对称的△A′B′C′；

    （2）连接 AA′，则△ACA′的面积为 ；

    （3）在直线 l 上找一点 P，使 PA+PB 的长最短，则这个最短长度为 ．

    查看答案和解析>>

    同步练习册答案