
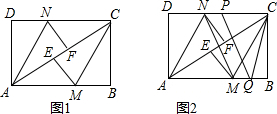
分析 (1)欲证明DN=BM,只需推知△ADN≌△CBM.根据折叠的性质得出∠DAN=∠NAC,∠BCM=∠ACM,从而根据AD∥BC可得出∠DAN=∠BCM,从而即可判断出△ADN≌△CBM.
(2)连接NE、MF,根据(1)的结论可得出NF=ME,再由∠NFE=∠MEF可判断出NF∥ME.
(3)设AC与MN的交点为O,EF=x,作QG⊥PC于G点,首先由勾股定理求出线段AC的长度,根据翻折变换知:AF=CE=3,结合线段间的和差关系求得EF=1;然后通过解Rt△CFN、Rt△NFE分别求得NF、NO的长,即NM=PQ=QC=2NO,结合图形得到:PC=2$\sqrt{P{Q}^{2}-Q{G}^{2}}$,所以AQ=AB-$\frac{1}{2}$PC.
解答  (1)证明:如图1,由折叠的性质得出∠DAN=∠NAC,∠BCM=∠ACM,
(1)证明:如图1,由折叠的性质得出∠DAN=∠NAC,∠BCM=∠ACM,
∵AD∥BC,
∴∠DAC=∠BCA,
∴∠DAN=∠BCM,
在Rt△ADN和Rt△CBM中,
∵$\left\{\begin{array}{l}{∠D=∠B=90°}\\{AD=BC}\\{∠DAM=∠BCM}\end{array}\right.$,
∴△ADN≌△CBM(ASA),
∴DN=BM;
(2)解:如图1,连接NE、MF,
∵由(1)知,△ADN≌△CBM,
∴NF=ME,
∵∠NFE=∠MEF,
∴NF∥ME,
∴四边形MFNE是平行四边形;
(3)解:如图2,设AC与MN的交点为O,EF=x,作QG⊥PC于G点,
∵AB=8,BC=6,
∴由勾股定理得到:AC=10,
∵AF=CE=BC=6,
∴2AF-EF=AC,即12-x=10,
解得x=2,
∴EF=2,
∴CF=4,
在Rt△CFN中,$\frac{NF}{CF}$=$\frac{BC}{AB}$=$\frac{3}{4}$,
解得NF=3,
∵OE=OF=$\frac{1}{2}$EF=1,
∴在Rt△NFO中,ON2=OF2+NF2,
∴ON=$\sqrt{10}$,
∴MN=2ON=2$\sqrt{10}$,
∵PQ∥MN,PN∥MQ,
∴四边形MQPN是平行四边形,
∴MN=PQ=2$\sqrt{10}$,
∵PQ=CQ,
∴△PQC是等腰三角形,
∴PG=CG,
在Rt△QPG中,
PG2=PQ2-QG2,即PG=$\sqrt{40-36}$=2,
又GC=PG=QB,
∴AQ=AB-BQ=AB-PG=6.
点评 本题主要考查翻折变换的知识点,还涉及平行四边形的证明,解答(3)问的关键是求出EF的长,此题难度较大,要熟练掌握此类试题的解答,此类题经常出现中考试卷中,请同学们关注.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
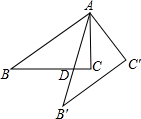 如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将△ABC绕点A逆时针旋转得到△AB′C′,AB′与BC相交于点D,当B′C′∥AB时,CD=$\frac{7}{8}$.
如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将△ABC绕点A逆时针旋转得到△AB′C′,AB′与BC相交于点D,当B′C′∥AB时,CD=$\frac{7}{8}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
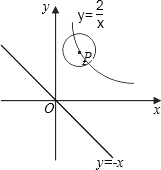 如图,直线y=-x与双曲线$y=\frac{2}{x}$(只在第一象限内的部分)在同一直角坐标系内,现有一个半径为1且圆心P在双曲线$y=\frac{2}{x}$上的一个动圆⊙P,⊙P在运动过程中圆上的点与直线y=-x的最近距离为1.
如图,直线y=-x与双曲线$y=\frac{2}{x}$(只在第一象限内的部分)在同一直角坐标系内,现有一个半径为1且圆心P在双曲线$y=\frac{2}{x}$上的一个动圆⊙P,⊙P在运动过程中圆上的点与直线y=-x的最近距离为1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 50元,30元 | B. | 50元,40元 | C. | 50元,50元 | D. | 55元,50元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com