
分析 根据解高次方程的方法可以解答此方程.
解答 解:$\left\{\begin{array}{l}{{x}^{4}+{y}^{2}+4=5yz}&{①}\\{{y}^{4}+{z}^{2}+4=5zx}&{②}\\{{z}^{4}+{x}^{2}+4=5xy}&{③}\end{array}\right.$,
通过观察可知:x=y=z,
则将x=y=z代入①,得
x4+x2+4=5x2,
∴x4-4x2+4=0,
∴(x2-2)2=0,
得x2=2,
∴x=$±\sqrt{2}$,
∴方程组的解为:$\left\{\begin{array}{l}{x=\sqrt{2}}\\{y=\sqrt{2}}\\{z=\sqrt{2}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\sqrt{2}}\\{y=-\sqrt{2}}\\{z=-\sqrt{2}}\end{array}\right.$.
点评 本题考查高次方程,解答本题的关键是明确解高次方程的方法.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:解答题
 (1)试帮助考古人员“修补”这个破碎的圆盘(保留作图痕迹,并写出作法)
(1)试帮助考古人员“修补”这个破碎的圆盘(保留作图痕迹,并写出作法)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
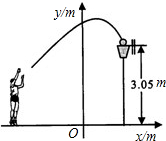 一位篮球运动员投篮,球沿抛物线y=-$\frac{1}{5}$x2+$\frac{7}{2}$运行,然后准确落入篮筐内,已知篮筐的中心距离底面的距离为3.05m.
一位篮球运动员投篮,球沿抛物线y=-$\frac{1}{5}$x2+$\frac{7}{2}$运行,然后准确落入篮筐内,已知篮筐的中心距离底面的距离为3.05m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
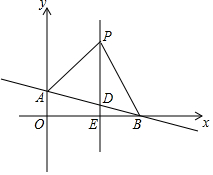 如图,在平面直角坐标系中,直线AB:y=kx+1(k≠0)交y轴于点A,交x轴于点B(3,0),平行于y轴的直线x=2交AB于点D,交x轴于点E,点P是直线x=2上一动点,且在点D的上方,设P(2,n).
如图,在平面直角坐标系中,直线AB:y=kx+1(k≠0)交y轴于点A,交x轴于点B(3,0),平行于y轴的直线x=2交AB于点D,交x轴于点E,点P是直线x=2上一动点,且在点D的上方,设P(2,n).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知正方形铁丝框ABCD边长为10,现使其变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形的面积为( )
如图,已知正方形铁丝框ABCD边长为10,现使其变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形的面积为( )| A. | 50 | B. | 100 | C. | 150 | D. | 200 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com