
【题目】如图,AD为△ABC的角平分线,DE⊥AC于E,DF⊥AB于F,EF交AD于点M.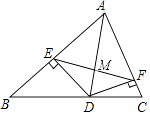
(1)试说明:MF=ME;
(2)若△ABC的面积为28cm2 , AB=20cm,AC=8cm,求DE的长.
【答案】
(1)解:∵AD为△ABC的觉平分线,DE⊥AC,DF⊥AB,
∴DF=DE.
在Rt△AED和Rt△AFD中, ![]() .
.
∴Rt△AED≌Rt△AFD.
∴AE=AF.
∵AE=AF,AD平分∠EAF,
∴EM=MF
(2)解:∵S△ABC=S△ABD+S△ACD,
∴ ![]() ABDF+
ABDF+ ![]() AC×DE=28,即10DF+4DE=28.
AC×DE=28,即10DF+4DE=28.
∵DF=DE,
∴14DE=28,解得DE=2
【解析】(1)依据角平分线的性质可得到ED=DF,然后利用HL可证明Rt△AED≌Rt△AFD,则AE=AF,最后依据等腰三角形三线合一的性质可得到MF=ME;
(2)由S△ABC=S△ABD+S△ACD列方程求解即可.
【考点精析】本题主要考查了角平分线的性质定理的相关知识点,需要掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点M,N分别是正五边形ABCDE的边BC,CD上的点,且BM=CN,AM交BN于点P,则∠APN的度数为( ) 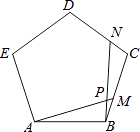
A.120°
B.118°
C.110°
D.108°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数统计结果如下表:
班级 | 参赛人数 | 中位数 | 方差 | 平均数 |
甲 | 55 | 149 | 191 | 135 |
乙 | 55 | 151 | 110 | 135 |
某同学分析上表后得出如下结论:
①甲、乙两班学生成绩平均水平相同;
②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字≥150个为优秀);
③甲班成绩的波动比乙班大,
上述结论正确的是( )
A.①②③
B.①②
C.①③
D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
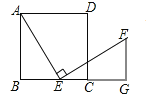
【题目】如图,在正方形ABCD中,点E(与点B、C不重合)是BC边上一点,将线段EA绕点E顺时针旋转90°到EF,过点F作BC的垂线交BC的延长线于点G,连接CF.
(1)求证:△ABE≌△EGF;
(2)若AB=2,S△ABE=2S△ECF,求BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】口袋里有红、绿、黄三种颜色的球,除颜色外其余均相同,其中有红球4个,绿球3个,任意摸出一个球是绿球的概率是 ![]() .试求:
.试求:
(1)口袋里黄球的个数;
(2)任意摸出一个球是黄球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数﹣22 , (﹣2)3 , ﹣|﹣2|, ![]() 按从小到大的顺序排列为( )
按从小到大的顺序排列为( )
A.(﹣2)3<﹣22<﹣|﹣2|< ![]()
B.![]() <﹣|﹣2|<﹣22<(﹣2)3
<﹣|﹣2|<﹣22<(﹣2)3
C.﹣|﹣2|< ![]() <﹣22<(﹣2)3
<﹣22<(﹣2)3
D.﹣22<(﹣2)3< ![]() <﹣|﹣2|
<﹣|﹣2|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)﹣8﹣12+2
(2)﹣18+(﹣7.5)﹣(﹣31)﹣12.5
(3)﹣ ![]() ﹣(+1
﹣(+1 ![]() )﹣(﹣
)﹣(﹣ ![]() )﹣(+4
)﹣(+4 ![]() )
)
(4)1﹣[(﹣1)﹣( ![]() )﹣(+5)﹣(
)﹣(+5)﹣( ![]() )]+|﹣4|.
)]+|﹣4|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com