
分析 利用有理数的减法,即可解答.
解答 解:P-Q=$\frac{{2}^{2002}+1}{{2}^{2003}+1}$-$\frac{{2}^{2003}+1}{{2}^{2004}+1}$
=$\frac{({2}^{2002}+1)({2}^{2004}+1)-({2}^{2003}+1)^{2}}{({2}^{2003}+1)({2}^{2004}+1)}$
=$\frac{{2}^{4006}+{2}^{2002}+{2}^{2004}+1-{2}^{4006}-{2}^{2004}-1}{({2}^{2003}+1)({2}^{2004}+1)}$
=$\frac{{2}^{2002}}{({2}^{2003}+1)({2}^{2004}+1)}$>0,
∴P>Q.
点评 本题考查了有理数的大小比较,解决本题的关键是作差比较大小.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
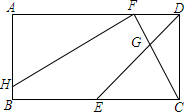 在矩形ABCD中,E为BC的中点,连接DE,F为AD上一点,连接CF,交DE于点G,过点F作HF⊥CF于点F,若$\frac{AB}{BC}=\frac{DG}{GE}$=$\frac{1}{2}$,DF=2.
在矩形ABCD中,E为BC的中点,连接DE,F为AD上一点,连接CF,交DE于点G,过点F作HF⊥CF于点F,若$\frac{AB}{BC}=\frac{DG}{GE}$=$\frac{1}{2}$,DF=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com