
���� ��1����P����M����N�ľ�����ȣ����Ե�PΪ�߶�MN���е㣬�Ӷ��ɵõ���P�����ꣻ
��2���ɷ�Ϊ��P�ڵ�M�����͵�P�ڵ�N���Ҳ࣬��P�ڵ�M�͵�N֮������������㣮
��3���ֱ���ݢٵ���M�͵�N�ڵ�Pͬ��ʱ���ڵ���M�͵�N�ڵ�P����ʱ������ɣ�
��� �⣺��1���ߵ�P����M����N�ľ�����ȣ�
���PΪMN���е㣮
���P��ʾ�ij�Ϊ-2��
��2���ٵ���P�ڵ�M�����ʱ��
��������ã�-6-x+2-x=10��
��ã�x=-7��
��P�ڵ�M�͵�N֮��ʱ��PN+PM=8���������⣮
�۵�P�ڵ�N���Ҳ�ʱ��x-��-6��+x-2=10��
��ã�x=3��
��x��ʾ������-7��3��
��3�����˶�t����ʱ����P��Ӧ������-6t����M��Ӧ������-6-2t����N��Ӧ������2-8t��
�ٵ���M�͵�N�ڵ�Pͬ��ʱ��
��PM=PN��
���M���N�غϣ�
��-6-2t=2-8t��
��ã�t=$\frac{4}{3}$��
�ڵ���M����N����ʱ��
��PM=PN��
��-6-2t+6t=6t-��2-8t����
��ã����t=-$\frac{4}{5}$����ȥ����
����N����M����ʱ����������ã�-6t-��2-8t��=-6-2t-��-6t��
��ã�t=2��
������������t=2��t=-$\frac{4}{5}$ʱ��P����M����N�ľ�����ȣ�
���� ������Ҫ�����������Ӧ���Լ�һԪһ�η��̵�Ӧ�ã�����M��Nλ�õIJ�ͬ���з������۵ó��ǽ���ؼ���


 ��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
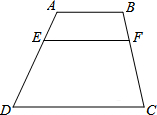 ��ͼ��AB��EF��CD��AB=3��CD=7��AE��ED=1��3����EF�ij���Ϊ4��
��ͼ��AB��EF��CD��AB=3��CD=7��AE��ED=1��3����EF�ij���Ϊ4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪ABΪ��O��ֱ����CD��AB�ڵ�D������O�ڵ�F��AC����O�ڵ�E��BE��CD�ڵ�G����֤��FD2=CD•GD��
��ͼ����֪ABΪ��O��ֱ����CD��AB�ڵ�D������O�ڵ�F��AC����O�ڵ�E��BE��CD�ڵ�G����֤��FD2=CD•GD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\overrightarrow{AD}$ | B�� | $\overrightarrow{BC}$ | C�� | $\overrightarrow{BA}$ | D�� | $\overrightarrow{BD}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| h��km�� | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
| t���棩 | 28 | 23.8 | 21.6 | 18.3 | 15 | 11.7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��ʽһ | ��ʽ�� | |
| ����� | 50Ԫ/�� | 10Ԫ/�� |
| ����ͨ���� | 0.30Ԫ/�� | 0.5Ԫ/�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com