
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 以2
以2![]() 的速度向点终点
的速度向点终点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 以1
以1![]() 的速度向点终点
的速度向点终点![]() 运动,它们到达终点后停止运动.
运动,它们到达终点后停止运动.
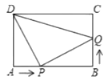
(1)几秒后,点![]() 、
、![]() 的距离是点
的距离是点![]() 、
、![]() 的距离的2倍;
的距离的2倍;
(2)几秒后,![]() 的面积是24
的面积是24![]() .
.
科目:初中数学 来源: 题型:
【题目】为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:
身高情况分组表(单位:cm)
组别 | 身高 |
A | x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | x≥170 |
根据图表提供的信息,回答下列问题:
(1)样本中,男生的身高众数在 组,中位数在 组;
(2)样本中,女生身高在E组的人数有 人;
(3)已知该校共有男生400人,女生380人,请估计身高在160≤x<170之间的学生约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD=4,AB=2.点E是AB的中点,点F是BC边上的任意一点(不与B、C重合),△EBF沿EF翻折,点B落在B'处,当DB'的长度最小时,BF的长度为________.
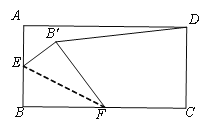
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
查看答案和解析>>
科目:初中数学 来源: 题型:
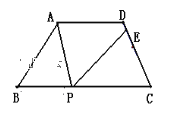
【题目】如图,等腰梯形ABCD中,AD∥BC,AD=3,BC=7,∠B=60°,P为下底BC上一点(不与B、C重合),连结AP,过点P作PE交CD于E,使得∠APE=∠B
(1)求证:△ABP∽△PCE
(2)在底边BC上是否存在一点P,使DE:EC=5:3?如果存在,求BP的长;如果不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
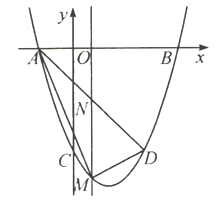
【题目】如图,抛物线y=(x1)2+n与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,3),点D与C关于抛物线的对称轴对称.
(1)求抛物线的解析式及点D的坐标;
(2)点P是抛物线上的一点,当△ABP的面积是8,求出点P的坐标;
(3)过直线AD下方的抛物线上一点M作y轴的平行线,与直线AD交于点N,已知M点的横坐标是m,试用含m的式子表示MN的长及△ADM的面积S,并求当MN的长最大时s的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
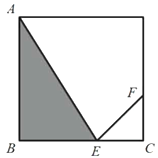
【题目】某人定制了一批地砖,每块地砖(如图(1)所示)是边长为0.5米的正方形![]() .点E、F分别在边
.点E、F分别在边![]() 和
和![]() 上,
上,![]() 、
、![]() 和四边形
和四边形![]() 均由单一材料制成,制成
均由单一材料制成,制成![]() 、
、![]() 和四边形
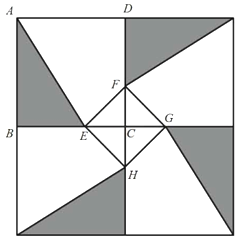
和四边形![]() 的三种材料的价格依次为每平方米30元、20元、10元.若将此种地砖按图(2)所示的形式铺设,且中间的阴影部分组成正方形
的三种材料的价格依次为每平方米30元、20元、10元.若将此种地砖按图(2)所示的形式铺设,且中间的阴影部分组成正方形![]() .设
.设![]() .
.
(1)![]() ________,
________,![]() _________.(用含有x的代数式表示).
_________.(用含有x的代数式表示).
(2)已知烧制该种地砖平均每块需加工费0.35元,若要![]() 长大于0.1米,且每块地砖的成本价为4元(成本价=材料费用+加工费用),则
长大于0.1米,且每块地砖的成本价为4元(成本价=材料费用+加工费用),则![]() 长应为多少米?
长应为多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com