
|
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
 今年某区为绿化车道,用25600元购买甲、乙两种树苗共500棵,且这批树苗的成活率恰好为92%.有关甲、乙两种树苗的信息如图所示.
今年某区为绿化车道,用25600元购买甲、乙两种树苗共500棵,且这批树苗的成活率恰好为92%.有关甲、乙两种树苗的信息如图所示.| 树苗类型 | 甲种树苗 | 乙种树苗 |
| 买树苗数量(单位:元) | x | 500-x |
| 买树苗的总费用(单位:元) |
查看答案和解析>>
科目:初中数学 来源: 题型:
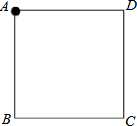 一枚棋子依次沿正方形ABCD的四个顶点A、B、C、D、A、B、C、D…移动,开始时棋子在A点(如图),然后根据骰子所掷点数移动棋子(如掷了1点,则移动1格到B,如掷6点,则移动6格到C等),移动后到达的点为新的出发点,再次进行同样的游戏.
一枚棋子依次沿正方形ABCD的四个顶点A、B、C、D、A、B、C、D…移动,开始时棋子在A点(如图),然后根据骰子所掷点数移动棋子(如掷了1点,则移动1格到B,如掷6点,则移动6格到C等),移动后到达的点为新的出发点,再次进行同样的游戏.查看答案和解析>>
科目:初中数学 来源: 题型:
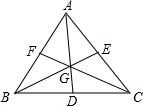 已知如图,点G是三角形ABC的三条中线AD,BE,CF的交点,求证:
已知如图,点G是三角形ABC的三条中线AD,BE,CF的交点,求证:| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com