
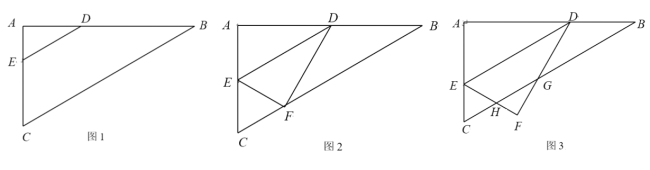
【题目】已知:如图1,在![]() 中,
中,![]() ,∠ABC=30°,
,∠ABC=30°,![]() ,点
,点![]() 、E分别是边
、E分别是边![]() 、AC上动点,点
、AC上动点,点![]() 不与点
不与点![]() 、
、![]() 重合,DE∥BC.
重合,DE∥BC.
(1)如图1,当AE=1时,求![]() 长;
长;
(2)如图2,把沿着直线![]() 翻折得到
翻折得到![]() ,设
,设![]()
①当点F落在斜边![]() 上时,求
上时,求![]() 的值;
的值;
② 如图3,当点F落在![]() 外部时,EF、DF分别与
外部时,EF、DF分别与![]() 相交于点H、G,如果△ABC和△DEF重叠部分的面积为
相交于点H、G,如果△ABC和△DEF重叠部分的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式及定义域.(直接写出答案)
的函数关系式及定义域.(直接写出答案)
【答案】(1)BD=![]() ;(2)①x=2;②
;(2)①x=2;②![]() .
.
【解析】
(1)根据DE∥BC,可得∠ADE=30°,然后分别利用三角函数求出AB和AD即可;
(2)①设![]() ,则AE=EF=4-x,然后证明△CEF是等边三角形即可解决问题;
,则AE=EF=4-x,然后证明△CEF是等边三角形即可解决问题;
②由①可知CE=x,AE=EF=4-x,△CEF是等边三角形,然后分别求出HF、FG和AD,利用三角形面积公式计算出![]() 和
和![]() ,进而得到
,进而得到![]() ,然后根据
,然后根据![]() 列式整理,并求出定义域即可.
列式整理,并求出定义域即可.
解:(1)∵![]() ,∠ABC=30°,
,∠ABC=30°,![]() ,AE=1,
,AE=1,
∴![]() ,
,
∵DE∥BC,
∴∠ADE=30°,
∴![]() ,
,
∴BD=AB-AD=![]() ;
;
(2)①设![]() ,则AE=4-x,
,则AE=4-x,
∴EF=4-x,
∵∠ADE=∠B =30°,
∴∠AED=∠C =60°,
∴∠CEF=180°-60°-60°=60°,
∴△CEF是等边三角形,
∴CE=EF,即x=4-x,
∴x=2;
②由①可知CE=x,AE=EF=4-x,△CEF是等边三角形,
∴HF=EF-EH=4-x-x=4-2x,∠FHG=∠CHE=60°,
∵∠F=∠A=90°,
∴FG=![]() HF=
HF=![]() ,
,
∴![]() ,
,
∵AE= 4-x,∠ADE=30°,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵当x=2时,点F落在斜边![]() 上,
上,
∴定义域为:![]() ,
,
即![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,![]() 三个顶点的坐标分别为
三个顶点的坐标分别为![]() ,
,![]() ,
,![]() .
.

(![]() )请画出将
)请画出将![]() 向左平移
向左平移![]() 个单位长度后得到的图形
个单位长度后得到的图形![]() .
.
(![]() )请画出
)请画出![]() 关于原点
关于原点![]() 成中心对称的图形
成中心对称的图形![]()
(![]() )在
)在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小,请直接写出点
的值最小,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
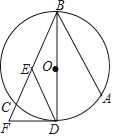
【题目】如图,A,B,C三点在⊙O上,直径BD平分∠ABC,过点D作DE∥AB交弦BC于点E,过点D作⊙O的切线交BC的延长线于点F.
(1)求证:EF=ED;
(2)如果半径为5,cos∠ABC=![]() ,求DF的长.
,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.

(1)判断线段DE、FG的位置关系,并说明理由;
(2)连结CG,求证:四边形CBEG是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=﹣![]() x2+bx+c的图象经过A(2,0),B(0,﹣6)两点,
x2+bx+c的图象经过A(2,0),B(0,﹣6)两点,
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与x轴交于点C,连接BA,BC,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】早上,小明从家里步行去学校,出发一段时间后,小明妈妈发现小明的作业本落在家里,便带上作业本骑车追赶,途中追上小明两人稍作停留,妈妈骑车返回,小明继续步行前往学校,两人同时到达.设小明在途的时间为x,两人之间的距离为y,则下列选项中的图象能大致反映y与x之间关系的是( )
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(感知)如图,点M是正方形ABCD的边BC上一点,点N是CD延长线上一点,且MA⊥AN,易证△ABM≌△ADN,进而证得∠AMB=∠AND.
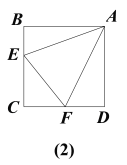
(应用)如图(1),在正方形ABCD中,点E、F分别在边BC、CD上,且∠EAF=45°.求证:∠BEA=∠AEF.
(拓展)如图(2),在四边形ABCD中,AB=AD,∠BAD=90°,∠B+∠D=180°,点E,F分别在边BC、CD上,∠EAF=45°.若∠BEA=50°,则∠AFD的大小为 度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图:经过已知直线外一点作这条直线的垂线.

已知:直线MN和直线外一点P.
求作:MN的垂线,使它经过点P.
(1)分步骤写出作图过程;
(2)说出所作直线就是求作垂线的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com