
【题目】如图,已知等边△ABC,AB=12,以AB为直径的半圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连结GD.
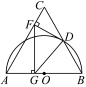
(1)求证:DF是⊙O的切线;
(2)求FG的长;(3)求tan∠FGD的值.
【答案】(1)证明过程见解析;(2)![]() ;(3)
;(3)![]()
【解析】
试题分析:(1)连接OD,根据等边三角形得出∠A=∠B=∠C=60°,根据OD=OB得到∠ODB=60°,得到OD∥AC,根据垂直得出切线;(2)根据中位线得出BD=CD=6,根据Rt△CDF的三角函数得出CF的长度,从而得到AF的长度,最后根据Rt△AFG的三角函数求出FG的长度;(3)过点D作DH⊥AB,根据垂直得出FG∥DH,根据Rt△BDH求出BH、DH的长度,然后得出∠GDH的正切值,从而得到∠FGD的正切值.
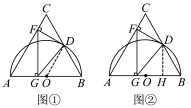
试题解析:(1)如图①,连结OD, ∵△ABC为等边三角形, ∴∠C=∠A=∠B=60°,
而OD=OB, ∴△ODB是等边三角形,∠ODB=60°, ∴∠ODB=∠C,
∴OD∥AC, ∵DF⊥AC,∴OD⊥DF,∴DF是⊙O的切线
(2)∵OD∥AC,点O为AB的中点,∴OD为△ABC的中位线,
∴BD=CD=6.在Rt△CDF中,∠C=60°,∴∠CDF=30°,
∴CF=CD=3,∴AF=AC-CF=12-3=9 在Rt△AFG中,∵∠A=60°,∴FG=AF·sinA=9×=
(3)如图②,过D作DH⊥AB于H.∵FG⊥AB,DH⊥AB,∴FG∥DH,∴∠FGD=∠GDH.在Rt△BDH中,∠B=60°,∴∠BDH=30°,∴BH=BD=3,DH=BH=3.∴tan∠GDH===,
∴tan∠FGD=tan∠GDH=


科目:初中数学 来源: 题型:
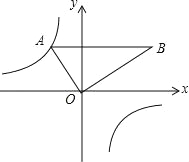
【题目】如图,把含30°角的三角板放置在如图所示的平面直角坐标系中,∠AOB=90°,∠B=30°,OA=2,斜边AB∥x轴,点A在双曲线上.
(1)求双曲线的解析式;
(2)把三角板AOB绕点A顺时针旋转,使得点O的对应点C落在x轴的负半轴上的对应线段为AD,试判断点D是否在双曲线上?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将一种商品A按标价的9折出售(即优惠10%)仍可获利润10%,若商品A的标价为33元,则该商品的进价为( )
A. 27元 B. 29.7元 C. 30.2元 D. 31元
查看答案和解析>>
科目:初中数学 来源: 题型:
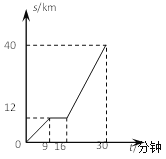
【题目】如图是某汽车行驶的路程s(km)与时间t(分钟) 的函数关系图。观察图中所提供的信息,解答下列问题:
(1)求汽车在前9分钟内的平均速度.
(2)汽车在中途停留的时间.
(3)求该汽车行驶30千米的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数y=-x+b的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=-x+b和y=x的图象于点C,D.
(1)求点A的坐标;(2)若OB=CD,求a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地计划用120~180天(含120与180天)的时间建设一项水利工程,工程需要运送的土石方总量为360万立方米.
(1)写出运输公司完成任务所需的时间y(单位:天)与平均每天的工作量x(单位:万立方米)之间的函数关系式,并给出自变量x的取值范围;
(2)由于工程进度的需要,实际平均每天运送土石方比原计划多5000立方米,工期比原计划减少了24天,原计划和实际平均每天运送土石方各是多少万立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
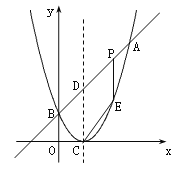
【题目】如图,已知二次函数图象的顶点坐标为C(1,0),直线![]() 与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴
与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴![]() 上.
上.
(1)求![]() 的值及这个二次函数的关系式;
的值及这个二次函数的关系式;
(2)P为线段AB上的一个动点(点P与A、B不重合),过P作![]() 轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为
轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为![]() ,点P的横坐标为
,点P的横坐标为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于y=2(x-3)2+2的图象,下列叙述正确的是( )
A. 顶点坐标为(-3,2) B. 对称轴为直线x=-3
C. 当x>3时,y随x的增大而增大 D. 当x>3时,y随x的增大而减小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com