
【题目】已知:如图![]() 的对角线
的对角线![]() 相交于点
相交于点![]() 过点
过点![]() 与
与![]() 分别相交于点
分别相交于点![]() ,
,
(1)求证:![]()
(2)若图中的条件都不变,将![]() 转动到图
转动到图![]() 的位置,那么上述结论是否成立?(不用证明)
的位置,那么上述结论是否成立?(不用证明)
(3)若将![]() 向两方延长与平行四边形的两对边的延长线分别相交(图
向两方延长与平行四边形的两对边的延长线分别相交(图![]() 和图
和图![]() ),结论是否成立,说明你的理由,(选用图
),结论是否成立,说明你的理由,(选用图![]() 进行证明)
进行证明)
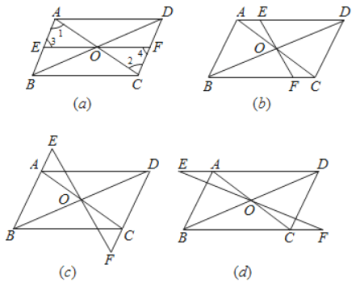
【答案】(1)见解析;(2)OE=OF,仍然成立;(3)OE=OF,仍然成立;理由见解析
【解析】
(1)证明△AOE≌△COF(ASA),即可解决问题.
(2)(3)结论成立,证明方法类似(1).
(1)证明:如图(a)中,
∵四边形ABCD是平行四边形,
∴OA=OC,AB∥CD,
∴∠1=∠2,
∵∠AOE=∠COF,
∴△AOE≌△COF(ASA),
∴OE=OF.
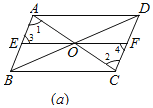
(2)解:结论成立.
理由:如图(b)中,
∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC,
∴∠EAO=∠FCO,
∵∠AOE=∠COF,
∴△AOE≌△COF(ASA),
∴OE=OF.
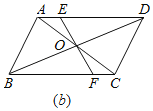
(3)解:结论成立.
如图(c)中,
∵四边形ABCD是平行四边形,
∴OA=OC,AB∥CD,
∴∠E=∠F,
∵∠AOE=∠COF,
∴△AOE≌△COF(ASA),
∴OE=OF.


科目:初中数学 来源: 题型:
【题目】在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化.如图,四边形的顶点在矩形的边上,且AN=AM=CP=CQ=xcm,已知矩形的边BC=200m,边AB=am,a为大于200的常数,设四边形MNPQ的面积为sm2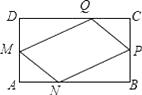
(1)求S关于x的函数关系式,并直接写出自变量x的取值范围.
(2)若a=400,求S的最大值,并求出此时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①垂线段最短;②同位角相等;③如果两条直线都与第三条直线平行,那么这两条直线也互相平行;④内错角相等,两直线平行;⑤经过一点有且只有一条直线与已知直线平行;⑥如果![]() =2,那么x=2.其中真命题有( )
=2,那么x=2.其中真命题有( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A、B、P的坐标分别为(1,0),(2,5),(4,2).若点C在第一象限内,且横坐标、纵坐标均为整数,P是△ABC的外心,则点C的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC,∠A=36°,∠B=72°,AC的垂直平分线分别交AC、AB于点D,E,则图中等腰三角形的个数为( )
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=12,点E在边CD上,且BG=CG,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②∠EAG=450;③CE=2DE;④AG∥CF;⑤S△FGC=![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com