
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() ,
,![]() 平分
平分![]() .给出下列结论:①
.给出下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .其中正确的结论是______.
.其中正确的结论是______.

【答案】①③④
【解析】
①根据等角的余角相等即可得到结果,故①正确;②如果∠EBC=∠C,则∠C=![]() ∠ABC,由于∠BAC=90°,那么∠C=30°,但∠C不一定等于30°,故②错误;③由BE、AG分别是∠ABC、∠DAC的平分线,得到∠ABF=∠EBD.由于∠AFE=∠BAD+∠FBA,∠AEB=∠C+∠EBD,得到∠AFE=∠AEB,可得③正确;④连接EG,先证明△ABN≌△GBN,得到AN=GN,证出△ANE≌△GNF,得∠NAE=∠NGF,进而得到GF∥AE,故④正确;⑤由AE=AF,AE=FG,而△AEF不一定是等边三角形,得到EF不一定等于AE,于是EF不一定等于FG,故⑤错误.
∠ABC,由于∠BAC=90°,那么∠C=30°,但∠C不一定等于30°,故②错误;③由BE、AG分别是∠ABC、∠DAC的平分线,得到∠ABF=∠EBD.由于∠AFE=∠BAD+∠FBA,∠AEB=∠C+∠EBD,得到∠AFE=∠AEB,可得③正确;④连接EG,先证明△ABN≌△GBN,得到AN=GN,证出△ANE≌△GNF,得∠NAE=∠NGF,进而得到GF∥AE,故④正确;⑤由AE=AF,AE=FG,而△AEF不一定是等边三角形,得到EF不一定等于AE,于是EF不一定等于FG,故⑤错误.
∵∠BAC=90°,AD⊥BC,
∴∠C+∠ABC=90°,∠C+∠DAC=90°,∠ABC+∠BAD=90°,
∴∠ABC=∠DAC,∠BAD=∠C,
故①正确;
若∠EBC=∠C,则∠C=![]() ∠ABC,
∠ABC,
∵∠BAC=90°,
那么∠C=30°,但∠C不一定等于30°,
故②错误;
∵BE、AG分别是∠ABC、∠DAC的平分线,
∴∠ABF=∠EBD,
∵∠AFE=∠BAD+∠ABF,∠AEB=∠C+∠EBD,
又∵∠BAD=∠C,
∴∠AFE=∠AEF,
∴AF=AE,
故③正确;
∵AG是∠DAC的平分线,AF=AE,
∴AN⊥BE,FN=EN,
在△ABN与△GBN中,
∵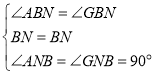 ,
,
∴△ABN≌△GBN(ASA),
∴AN=GN,
又∵FN=EN,∠ANE=∠GNF,
∴△ANE≌△GNF(SAS),
∴∠NAE=∠NGF,
∴GF∥AE,即GF∥AC,
故④正确;
∵AE=AF,AE=FG,
而△AEF不一定是等边三角形,
∴EF不一定等于AE,
∴EF不一定等于FG,
故⑤错误.
故答案为:①③④.


科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于( ) 
A.55°
B.70°
C.125°
D.145°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有A、B两种型号的客车共11辆,它们的载客量(不含司机)、日租金、车辆数如下表所示,已知这11辆客车满载时可搭载乘客350人.
A型客车 | B型客车 | |
载客量(人/辆) | 40 | 25 |
日租金(元/辆) | 320 | 200 |
车辆数(辆) | a | b |
(1)求a、b的值;
(2)某校七年级师生周日集体参加社会实践,计划租用A、B两种型号的客车共6辆,且租车总费用不超过1700元.
①最多能租用A型客车多少辆?
②若七年级师生共195人,写出所有的租车方案,并确定最省钱的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,E,F,G,H分别是四边形ABCD的边AB,BC,CD,AD的中点.
(1)探究1:连接对角线AC,BD由三角形中位线定理及平行四边形的判定定理易得四边形EFGH为 (不需要证明);
(2)探究2:观察猜想:
①当四边形ABCD的对角线AC,BD满足条件 时,四边形EFGH是菱形;
②当四边形ABCD的对角线AC,BD满足条件 时,四边形EFGH为矩形.
(3)探究3:当四边形ABCD满足什么条件时,四边形EFGH为正方形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
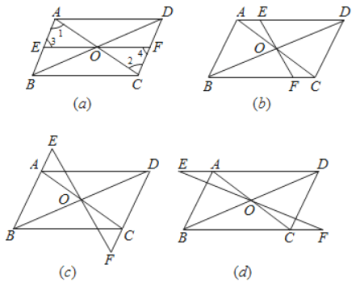
【题目】已知:如图![]() 的对角线
的对角线![]() 相交于点
相交于点![]() 过点
过点![]() 与
与![]() 分别相交于点
分别相交于点![]() ,
,
(1)求证:![]()
(2)若图中的条件都不变,将![]() 转动到图
转动到图![]() 的位置,那么上述结论是否成立?(不用证明)
的位置,那么上述结论是否成立?(不用证明)
(3)若将![]() 向两方延长与平行四边形的两对边的延长线分别相交(图
向两方延长与平行四边形的两对边的延长线分别相交(图![]() 和图
和图![]() ),结论是否成立,说明你的理由,(选用图
),结论是否成立,说明你的理由,(选用图![]() 进行证明)
进行证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O的内接三角形,∠C=30°,⊙O的半径为5,若点P是⊙O上的一点,在△ABP中,PB=AB,则PA的长为( )
A.5
B.![]()
C.5 ![]()
D.5 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.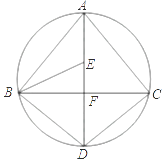
(1)求证:BD=CD;
(2)请判断B,E,C三点是否在以D为圆心,以DB为半径的圆上?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C为线段AB上一点,△ACM,△CBN是等边三角形,直线AN,MC交于点E,直线BM,CN交于点F. 
(1)求证:AN=MB;
(2)求证:△CEF为等边三角形;
(3)将△ACM绕点C按逆时针方向旋转90°,其他条件不变,在(2)中画出符合要求的图形,并判断(1)(2)题中的两结论是否依然成立.并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘船由A港沿北偏东60°方向航行10km至B港,然后再沿北偏西30°方向航行10km至C港.
(1)求A,C两港之间的距离(结果保留到0.1km,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732);
≈1.732);
(2)确定C港在A港的什么方向.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com