
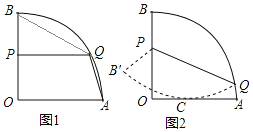
【题目】如图1,扇形OAB的半径为4,∠AOB=90°,P是半径OB上一动点,Q是![]() 上一动点.
上一动点.
(1)连接AQ、BQ、PQ,则∠AQB的度数为 ;
(2)当P是OB中点,且PQ∥OA时,求![]() 的长;
的长;
(3)如图2,将扇形OAB沿PQ对折,使折叠后的![]() 恰好与半径OA相切于点C.若OP=3,求点O到折痕PQ的距离.
恰好与半径OA相切于点C.若OP=3,求点O到折痕PQ的距离.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)如图,补全图形,运用圆内接四边形的性质求解即可;
(2)要想求![]() 弧长,就得求
弧长,就得求![]() 所对的圆心角的度数,所以要连接OQ,构成圆心角,利用直角三角形直角边是斜边的一半,则这条直角边所对的锐角为30°求出∠1=30°,再利用平行线截得内错角相等得出∠2的度数,代入弧长公式计算即可.
所对的圆心角的度数,所以要连接OQ,构成圆心角,利用直角三角形直角边是斜边的一半,则这条直角边所对的锐角为30°求出∠1=30°,再利用平行线截得内错角相等得出∠2的度数,代入弧长公式计算即可.
(3)先找点O关于PQ的对称点O′,连接OO′、O′B、O′C、O′P,证明四边形OCO′B是矩形,由勾股定理求O′B,从而求出OO′的长,则OM=![]() OO′=
OO′=![]() .
.
(1)补全图形如图所示,
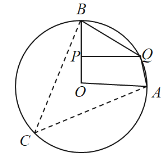
∵∠AOB=90°,
∴∠BCA=45°,
∵四边形ACBQ是圆内接四边形,
∴∠AQB+∠C=180°,
∴∠AQB=180°-∠C=135°
故答案为:135°;
(2)如图1,连接OQ,
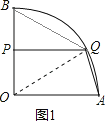
∵扇形OAB的半径为4且P是OB中点,
∴OP=2,OQ=4,
∵PQ∥OA,
∴∠BPQ=∠AOB=90°,
∴∠OQP=30°,
∴∠AOQ=∠OQP=30°,
∴![]() 的长=
的长=![]() =
=![]() π;
π;
(3)如图2,找点O关于PQ的对称点O′,连接OO′、O′B、O′C、O′P,ON,
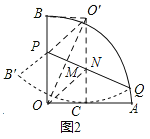
则OM=O′M,OO′⊥PQ,O′P=OP=3,点O′是![]() 所在圆的圆心,
所在圆的圆心,
∴O′C=OB=4,
∵折叠后的弧QB′恰好与半径OA相切于C点,
∴O′C⊥AO,
∴O′C∥OB,
∴∠POO'=∠CO'M=∠PO'M,
∵∠PMO'=∠QMO'=90°,
∴∠O'PM=∠MNO',
∴O'P=O'N=OP=3,
∴四边形OPO'N是平行四边形,
∴O'P=ON,
∵O与O'关于PQ对称,
∴ON=O'N=3,
∴BP=CN=4﹣3=1,
∵PN⊥OO',
∴∠MNO'=∠MNO,
∴∠BPO'=∠CNO,
∴△O'BP≌△OCN(SAS),
∴∠O'BP=∠OCN=90°,
∴四边形OCO′B是矩形,
在Rt△O′BP中,O′B=![]() =2
=2![]() ,
,
在Rt△OBO′中,OO′=![]() =2
=2![]() ,
,
∴OM=![]() OO′=
OO′=![]() ×2
×2![]() =
=![]() ,
,
即O到折痕PQ的距离为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】有专家指出:人为型空气污染(如汽车尾气排放等)是雾霾天气的重要成因.某校为倡议“每人少开一天车,共建绿色家园”,想了解学生上学的交通方式.九年级(8)班的5名同学联合设计了一份调查问卷.对该校部分学生进行了随机调查.按A(骑自行车)、B(乘公交车)、C(步行)、D(乘私家车)、E(其他方式)设置选项,要求被调查同学从中单选.并将调查结果绘制成条形统计图1和扇形统计图2,根据以上信息,解答下列问题:
(1)本次接受调查的总人数是 人,扇形统计图中“骑自行车”所在扇形的圆心角度数是 度,请补全条形统计图;
(2)已知这5名学生中有2名女同学,要从这5名学生中任选两名同学汇报调查结果.请用列表法或画树状图的方法,求出恰好选出1名男生和1名女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
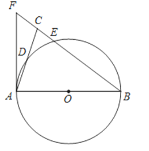
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,BC的延长线与⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE,AF的长.
,CE:EB=1:4,求CE,AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象与x轴负半轴交于点A(-1,0),与y轴正半轴交与点B,顶点为P,且OB=3OA,一次函数y=kx+b的图象经过A、B.
的图象与x轴负半轴交于点A(-1,0),与y轴正半轴交与点B,顶点为P,且OB=3OA,一次函数y=kx+b的图象经过A、B.
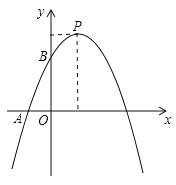
(1) 求一次函数解析式;
(2)求顶点P的坐标;
(3)平移直线AB使其过点P,如果点M在平移后的直线上,且![]() ,求点M坐标;
,求点M坐标;
(4)设抛物线的对称轴交x轴与点E,联结AP交y轴与点D,若点Q、N分别为两线段PE、PD上的动点,联结QD、QN,请直接写出QD+QN的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 有一种用“☆”定义的新运算,对于任意实数a,b,都有a☆b=b2+2a+1.例如7☆4=42+2×7+1=31.
(1)已知﹣m☆3的结果是﹣4,则m= .
(2)将两个实数2n和n﹣2用这种新定义“☆”加以运算,结果为9,则n的值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个边长分别为![]() 和
和![]() 的正方形如图放置(图1),其未叠合部分(阴影)面积为
的正方形如图放置(图1),其未叠合部分(阴影)面积为![]() ;若再在图1中大正方形的右下角摆放一个边长为
;若再在图1中大正方形的右下角摆放一个边长为![]() 的小正方形(如图2),两个小正方形叠合部分(阴影)面积为
的小正方形(如图2),两个小正方形叠合部分(阴影)面积为![]() .
.



(1)用含![]() 、
、![]() 的代数式分别表示
的代数式分别表示![]() 、
、![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)当![]() 时,求出图3中阴影部分的面积
时,求出图3中阴影部分的面积![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
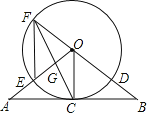
【题目】如图,在△OAB中,OA=OB,C为AB中点,以O为圆心,OC长为半径作圆,AO与⊙O交于点E,直线OB与⊙O交于点F和D,连接EF.CF,CF与OA交于点G.
(1)求证:直线AB是![]() 的切线;
的切线;
(2)求证:ODEG=OGEF;
(3)若AB=4BD,求sinA的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
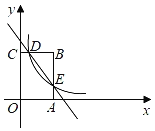
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(4,6).反比例函数y=![]() (x>0)的图象经过BC的中点D,与AB交于点E,连接DE.
(x>0)的图象经过BC的中点D,与AB交于点E,连接DE.
(1)求k的值;
(2)求直线DE的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据某网站调查,2019年网民最关注的热点话题分别是:消费、教育、环保、反腐及其他共五类,根据调查的部分相关数据绘制的统计图如图:
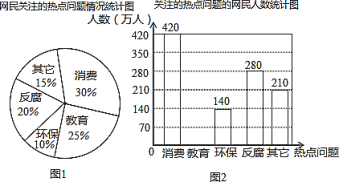
根据以上信息解答下列问题:
(1)请补全条形图,并在图中标明相应数据.
(2)若某市中心城区约有90万人口,请你估计该市中心城区最关注教育问题的人数约有多少万人?
(3)据统计,2017年网民最关注教育问题的人数所占百分比约为10%,则从2017年到2019年关注该问题网民数的年平均增长率约为多少?(已知2017~2019年每年接受调查的网民人数相同,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com