
【题目】如图,在一笔直的沿湖道路上有A、B两个游船码头,观光岛屿C在码头A北偏东60°的方向,在码头B北偏东15°的方向,AB=4km.
(1)求观光岛屿C与码头A之间的距离(即AC的长);
(2)游客小明准备从观光岛屿C乘船沿湖回到码头A或沿CB回到码头B,若开往码头A、B的游船速度相同,设开往码头A、B所用的时间分别是t1、t2,求![]() 的值.(结果保留根号)
的值.(结果保留根号)

【答案】(1)(2![]() +2)km;(2)
+2)km;(2)![]()
【解析】
(1)过点B作BD⊥AC于点D,先解Rt△ABD,求出AD,再解Rt△ABD,求出CD,再根据AC=AD+CD求解即可;
(2)先解Rt△BCD,求出BC,再根据速度相同,时间与路程成正比即可求解.
(1)如图,过点B作BD⊥AC于点D.
根据题意得∠CAB=30°,∠ABC=105°,
∵BD⊥AC,
∴∠ADB=90°,
∴∠ABD=60°,
∴∠CBD=45°,
在Rt△ABD中,∠CAB=30°,AB=4km,
∴BD=ABsin30°=2km,AD=ABcos30°=2![]() km,
km,
在Rt△BCD中,∠CBD=45°,
∴CD=BDtan45°=2km,
AC=AD+CD=(2![]() +2)km;
+2)km;
(2)在Rt△BCD中,∠CBD=45°,
∴BC=![]() BD=2
BD=2![]() km,
km,
∵速度相同,
∴![]() =
=![]() =
=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长均为1,建立如图所示的直角坐标系,已知两点A(0,2),B(4,1)

(1)请在x轴上画出一点P,使得PA+PB的值最小;
(2)请直接写出:点P的坐标 ;PA+PB的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在△ABC中,BO,CO分别平分∠ABC,∠ACB,交于O,CE为外角∠ACD的平分线,BO的延长线交CE于点E,记∠BAC=∠1,∠BEC=∠2,则以下结论①∠1=2∠2,②∠BOC=3∠2,③∠BOC=90°+∠1,④∠BOC=90°+∠2正确的是( )
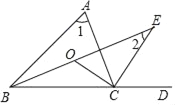
A. ①②③ B. ①③④ C. ①④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠A>∠B,分别以点A,C为圆心,大于![]() AC长为半径画弧,两弧交于点P,点Q,作直线PQ交AB于点D,再分别以点B,D为圆心,大于
AC长为半径画弧,两弧交于点P,点Q,作直线PQ交AB于点D,再分别以点B,D为圆心,大于![]() BD长为半径画弧,两弧交于点M,点N,作直线MN交BC于点E,若△CDE是等边三角形,则∠A=_____.
BD长为半径画弧,两弧交于点M,点N,作直线MN交BC于点E,若△CDE是等边三角形,则∠A=_____.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,甲车到达C地后因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图2,结合图象信息解答下列问题:
(1)乙车的速度是 千米/时,乙车行驶的时间t= 小时;
(2)求甲车从C地按原路原速返回A地的过程中,甲车距它出发地的路程y与它出发的时间x的函数关系式;
(3)直接写出甲车出发多长时间两车相距80千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,在四边形ABCD是矩形,点E是AD的中点,求证:EB=EC.

(2)如图,AB与![]() 相切于C,
相切于C,![]() ,⊙O的半径为6,AB=16,求OA的长.
,⊙O的半径为6,AB=16,求OA的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线AB∥CD.
(1)如图1,直接写出∠ABE,∠CDE和∠BED之间的数量关系是 .
(2)如图2,BF,DF分别平分∠ABE,∠CDE,那么∠BFD和∠BED有怎样的数量关系?请说明理由.
(3)如图3,点E在直线BD的右侧,BF,DF仍平分∠ABE,∠CDE,请直接写出∠BFD和∠BED的数量关系 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图,图象过点(﹣1,0),对称轴为直线
的部分图象如图,图象过点(﹣1,0),对称轴为直线![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④当
;④当![]() 时,
时, ![]() 随
随![]() 的增大而增大.其中正确的结论有( )
的增大而增大.其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com