
【题目】如图,方格纸中每个小正方形的边长均为1,建立如图所示的直角坐标系,已知两点A(0,2),B(4,1)

(1)请在x轴上画出一点P,使得PA+PB的值最小;
(2)请直接写出:点P的坐标 ;PA+PB的最小值为 .
【答案】(1)详见解析;(2)P点坐标为(![]() ,0),PA+PB的最小值为5.
,0),PA+PB的最小值为5.
【解析】
(1)作A点关于x轴的对称点A′,连结BA′交x轴于P点,利用对称的性质得到PA=PA′,则PA+PB=PA′+PB=BA′,于是利用两点之间线段最短可判断P点满足条件;
(2)先写出点A′的坐标为(0,﹣2),再利用待定系数法求出直线BA′的解析式为y=![]() x﹣2,然后解方程
x﹣2,然后解方程![]() x﹣2=0得P点坐标,然后利用两点间的距离公式求出BA′即可.
x﹣2=0得P点坐标,然后利用两点间的距离公式求出BA′即可.
解:(1)如图,点P为所作;
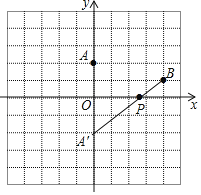
(2)A点关于x轴对称的点A′的坐标为(0,﹣2),
设直线BA′的解析式为y=kx+b,
把A′(0,﹣2),B(4,1)得![]() ,解得,
,解得,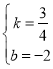
∴直线BA′的解析式为y=![]() x﹣2,
x﹣2,
当y=0时,![]() x﹣2=0,解得x=
x﹣2=0,解得x=![]() ,
,
∴P点坐标为(![]() ,0),
,0),
PA+PB的最小值=![]() ,
,
故答案为:(![]() ,0),5.
,0),5.


科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )

A. 76° B. 78° C. 80° D. 82°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将长方形纸片ABCD如图折叠,B、C 两点恰好重合落在AD 边上的同一点P 处,折痕分别是MH、NG,已知∠MPN=90°,且PM=3,MN=5.则△PGN面积为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠CAB=30°.以AB长为一边作△ABD,且AD=BD,∠ADB=90°,取AB中点E,连DE、CE、CD.则∠EDC= °.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C,已知A(﹣1,0),C(0,3)
(1)求该抛物线的表达式;
(2)求BC的解析式;
(3)点M是对称轴右侧点B左侧的抛物线上一个动点,当点M运动到什么位置时,△BCM的面积最大?求△BCM面积的最大值及此时点M的坐标.
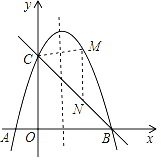
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角三角形纸片ABC中,∠ACB=90°,AC=2,BC=4,点D在边AB上,以CD为折痕将△CBD折叠得到△CPD,CP与边AB交于点E,若△DEP为直角三角形,则BD的长是_____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场准备进一批两种不同型号的衣服,已知购进A种型号衣服9件,B种型号衣服10件,则共需1810元;若购进A种型号衣服12件,B种型号衣服8件,共需1880元;已知销售一件A型号衣服可获利18元,销售一件B型号衣服可获利30元,要使在这次销售中获利不少于699元,且A型号衣服不多于28件.
(1)求A、B型号衣服进价各是多少元?
(2)若已知购进A型号衣服是B型号衣服的2倍还多4件,则商店在这次进货中可有几种方案并简述购货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题选择一个,九年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.

(1)求共抽取了多少名学生的征文;
(2)将上面的条形统计图补充完整;
(3)在扇形统计图中,选择“爱国”主题所对应的圆心角是多少;
(4)如果该校九年级共有1200名学生,请估计选择以“友善”为主题的九年级学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一笔直的沿湖道路上有A、B两个游船码头,观光岛屿C在码头A北偏东60°的方向,在码头B北偏东15°的方向,AB=4km.
(1)求观光岛屿C与码头A之间的距离(即AC的长);
(2)游客小明准备从观光岛屿C乘船沿湖回到码头A或沿CB回到码头B,若开往码头A、B的游船速度相同,设开往码头A、B所用的时间分别是t1、t2,求![]() 的值.(结果保留根号)
的值.(结果保留根号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com