
 如图,点D为等边三角形ABC外一点,BD=DA,BE=BA,∠DBE=∠DBC,则∠E的度数是( )
如图,点D为等边三角形ABC外一点,BD=DA,BE=BA,∠DBE=∠DBC,则∠E的度数是( )| A、10° | B、20° |
| C、30° | D、40° |
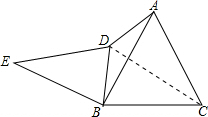 解:连接DC,
解:连接DC,
|


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 如图已知,CE⊥AB,BF⊥AC,BF交CE于点D,且BD=CD.
如图已知,CE⊥AB,BF⊥AC,BF交CE于点D,且BD=CD.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,下列结论:①△DEF是等腰直角三角形;②四边形CDFE可能为正方形;③DE长度的最小值为4;④四边形CDFE的面积保持不变;⑤△CDE面积的最大值为8.其中正确的结论是
如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,下列结论:①△DEF是等腰直角三角形;②四边形CDFE可能为正方形;③DE长度的最小值为4;④四边形CDFE的面积保持不变;⑤△CDE面积的最大值为8.其中正确的结论是查看答案和解析>>
科目:初中数学 来源: 题型:
| A、日光灯管厂要检测一批灯管的使用寿命,采用普查方式 |
| B、了解海门市每天的流动人口数,采用抽样调查方式 |
| C、了解海门市民对各类电视节目的喜爱情况,采用普查方式 |
| D、旅客上飞机前的安检,采用抽样调查方式 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com