
如图,已知:在平行四边形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.求证:
(1)△AEH≌△CGF;
(2)四边形EFGH是菱形.
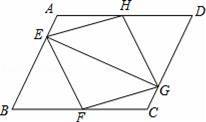

【考点】平行四边形的性质;全等三角形的判定与性质;菱形的判定.
【专题】证明题.
【分析】(1)由全等三角形的判定定理SAS证得结论;
(2)易证四边形EFGH是平行四边形,那么EF∥GH,那么∠HGE=∠FEG,而EG是角平分线,易得∠HEG=∠FEG,根据等量代换可得∠HEG=∠HGE,从而有HE=HG,易证四边形EFGH是菱形.
【解答】(1)证明:如图,∵四边形ABCD是平行四边形,
∴∠A=∠C,
在△AEH与△CGF中,
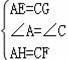
 ,
,
∴△AEH≌△CGF(SAS);
(2)∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠D.
又∵AE=CG,AH=CF,
∴BE=DG,BF=DH,
在△BEF与△DGH中,
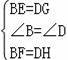

∴△BEF≌△DGH(SAS),
∴EF=GH.
又由(1)知,△AEH≌△CGF,
∴EH=GF,
∴四边形EFGH是平行四边形,
∴HG∥EF,
∴∠HGE=∠FEG,
∵EG平分∠HEF,
∴∠HEG=∠FEG,
∴∠HEG=∠HGE,
∴HE=HG,
∴四边形EFGH是菱形.


【点评】本题考查了全等三角形的判定和性质、平行四边形的判定和性质、菱形的判定.解题的关键是掌握两组对边相等的四边形是平行四边形,一组邻边相等的平行四边形是菱形.


科目:初中数学 来源: 题型:
某校为了了解本校七年级学生课外阅读的喜好,随机抽取该校七年级部分学生进行问卷调査(每人只选一种书籍).如图是整理数据后绘制的两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:(8分)
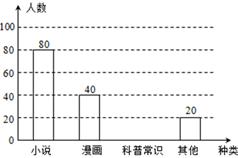
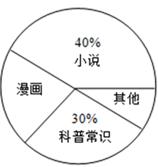
(1)这次活动一共调查了________名学生;
(2)在扇形统计图中,“其他”所在扇形的百分比等于__________;
(3)补全条形统计图;
(4)若该年级有600名学生,请你估计该年级喜欢“科普常识”的学生人数约是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB是⊙O的直径,
 =
=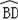
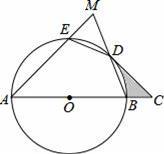
 ,连接ED、BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.
,连接ED、BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.
(1)若OA=CD=2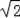
 ,求阴影部分的面积;
,求阴影部分的面积;
(2)求证:DE=DM.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com