
分析 (1)作AB的垂直平分线,然后在垂直平分线上找出到x轴的距离为5的点即为P点,这样△ABP为等腰直角三角形;
(2)利用画法直接写出P点坐标;
(3)以点P为圆心,PA为半径作圆交y轴于C点,作PH⊥y轴于H,如图,利用圆周角定理可判断∠ACB=$\frac{1}{2}$∠APB=45°,接着根据勾股定理计算出CH=7,于是可得到C(0,12),同理可得C′(0,-12).
解答 解:(1)如图,△ABP和△ABP′为所作;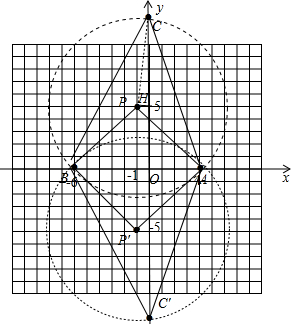
(2)点P在AB的垂直平分线上,则P点的横坐标为-1,
而AB=10,点P到AB的距离为$\frac{1}{2}$AB,
所以P点坐标为(-1,5)或(-1,-5);
(3)以点P为圆心,PA为半径作圆交y轴于C点,作PH⊥y轴于H,如图,
则∠ACB=$\frac{1}{2}$∠APB=45°,
PC=PA=5$\sqrt{2}$,PH=1,
在Rt△PCH中,CH=$\sqrt{(5\sqrt{2})^{2}-{1}^{2}}$=7,
∴C(0,12),
同理可得C′(0,-12),
即满足条件的C点坐标为(0,12)或(0,-12).
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.也考查了等腰直角三角形和圆周角定理.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
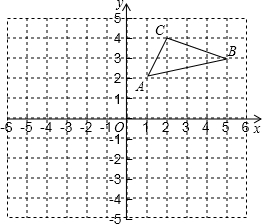 如图,在平行直角坐标系中,△ABC的三个顶点的坐标为A(1,2),B(5,3),C(2,4).
如图,在平行直角坐标系中,△ABC的三个顶点的坐标为A(1,2),B(5,3),C(2,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
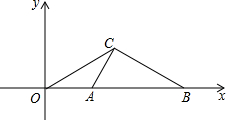 如图,已知点A(2,0),B(6,0),∠ACB是直角,△OCA∽△OBC.
如图,已知点A(2,0),B(6,0),∠ACB是直角,△OCA∽△OBC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
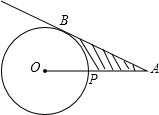 如图,已知A为⊙O外一点,连接OA,交⊙O于P,AB是⊙O的切线,B是切点,且PO=2cm,AB=2$\sqrt{3}$cm,求阴影部分的面积.
如图,已知A为⊙O外一点,连接OA,交⊙O于P,AB是⊙O的切线,B是切点,且PO=2cm,AB=2$\sqrt{3}$cm,求阴影部分的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +0.60 | +0.65 | -0.30 | -0.55 | -0.60 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com