
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 甲班 | 8 | 7 | 7 | 4 | 8 | 7 | 8 | 8 | 8 | 8 |
| 乙班 | 7 | 8 | 8 | 10 | 7 | 7 | 8 | 7 | 7 | 7 |
分析 (1)直接利用平均数求法得出两个班级的平均分即可;
(2)去掉一个最高分,再去掉一个最低分,再求平均数,进而得出答案.
解答 解:(1)$\overline{{x}_{甲}}$=$\frac{1}{10}$(8+7+7+4+8+7+8+8+8+8)=7.3(分),
$\overline{{x}_{乙}}$=$\frac{1}{10}$(7+8+8+10+7+7+8+7+7+7)=7.6(分)
这样乙获胜,这种方法不公平,因为平均数受极端值的影响;
(2)应该去掉一个最高分,再去掉一个最低分,再求平均数,对参赛班级更为公平,
$\overline{{x}_{甲}}$=$\frac{1}{8}$(8+7+7+8+7+8+8+8)=7.625(分),
$\overline{{x}_{乙}}$=$\frac{1}{8}$(7+8+8+7+7+8+7+7)=7.375(分),
这样甲获胜.
点评 此题主要考查了游戏公平性以及平均数求法,正确理解平均数的意义是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
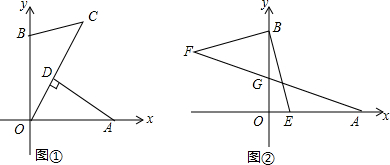
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
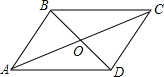 如图,?ABCD周长为100cm,AC与BD交于O,△OAB的周长与△OBC的周长的和为122cm,AC:BD=5:4,求AC与BD的长.
如图,?ABCD周长为100cm,AC与BD交于O,△OAB的周长与△OBC的周长的和为122cm,AC:BD=5:4,求AC与BD的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
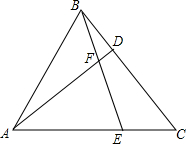 如图,在等边△ABC中,点D、E分别在BC、AC边上,BD=CE,AD与BE相交于点F.
如图,在等边△ABC中,点D、E分别在BC、AC边上,BD=CE,AD与BE相交于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com