
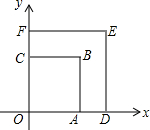
 如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为2:3,点B、E在第一象限,若点A的坐标为(1,0),则点E的坐标是( )
如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为2:3,点B、E在第一象限,若点A的坐标为(1,0),则点E的坐标是( )| A. | ($\sqrt{2},0$) | B. | ($\frac{3}{2},\frac{3}{2}$) | C. | ($\sqrt{2},\sqrt{2}$) | D. | (2,2) |
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x+2分别交x轴、y轴于A、B两点,点P(1,m)在△AOB的形内(不包含边界),则m的值可能是1.(填一个即可)
如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x+2分别交x轴、y轴于A、B两点,点P(1,m)在△AOB的形内(不包含边界),则m的值可能是1.(填一个即可)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
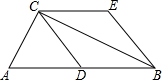 如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,过点B作BE∥CD,过点C作CE∥AB,BE,CE相交于点E.
如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,过点B作BE∥CD,过点C作CE∥AB,BE,CE相交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
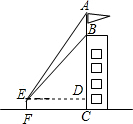 如图,为测量某建筑物BC上旗杆AB的高度,在离该建筑物底部12m的点F处,从E点观测旗杆的顶端A处和底端B处,视线与水平线夹角∠AED为52°,∠BED为45°,目高EF为1.6m.
如图,为测量某建筑物BC上旗杆AB的高度,在离该建筑物底部12m的点F处,从E点观测旗杆的顶端A处和底端B处,视线与水平线夹角∠AED为52°,∠BED为45°,目高EF为1.6m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 有一种足球是由32块黑白相间的牛皮缝制而成的(如图),黑皮可看作正五边形,白皮可看作正六边形.设白皮有x块,则黑皮有(32-x)块,要求出黑皮、白皮的块数,列出的方程是( )
有一种足球是由32块黑白相间的牛皮缝制而成的(如图),黑皮可看作正五边形,白皮可看作正六边形.设白皮有x块,则黑皮有(32-x)块,要求出黑皮、白皮的块数,列出的方程是( )| A. | 3x=32-x | B. | 3x=5(32-x) | C. | 5x=3(32-x ) | D. | 6x=32-x |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
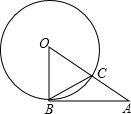 如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BCA=115°,则∠A的度数为( )
如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BCA=115°,则∠A的度数为( )| A. | 40° | B. | 45° | C. | 50° | D. | 55° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com