
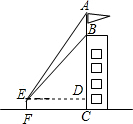
 如图,为测量某建筑物BC上旗杆AB的高度,在离该建筑物底部12m的点F处,从E点观测旗杆的顶端A处和底端B处,视线与水平线夹角∠AED为52°,∠BED为45°,目高EF为1.6m.
如图,为测量某建筑物BC上旗杆AB的高度,在离该建筑物底部12m的点F处,从E点观测旗杆的顶端A处和底端B处,视线与水平线夹角∠AED为52°,∠BED为45°,目高EF为1.6m.分析 (1)先过点E作ED⊥BC于D,由已知底部B的仰角为45°得BD=ED=FC=12,DC=EF=1.6,从而求出BC;
(2)由已知由E点观测到旗杆顶部A的仰角为52°可求出AD,则AB=AD-BD.
解答 解:(1)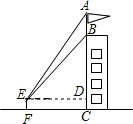 根据题意得:EF⊥FC,ED∥FC,
根据题意得:EF⊥FC,ED∥FC,
∴四边形CDEF是矩形,
∵∠BED=45°,
∴∠EBD=45°,
∴BD=ED=FC=12,
∴BC=BD+DC=BD+EF=12+1.6=13.6,
答:建筑物BC的高度为13m;
(2)∵∠AED=52°,
∴AD=ED•tan52°
≈12×1.28≈15.36m,
∴AB=AD-BD=15.36-12=3.4m,
答:旗杆AB的高度约为3.4m.
点评 此题考查的知识点是解直角三角形的应用,解题的关键是把实际问题转化为解直角三角形问题,先得到等腰直角三角形,再根据三角函数求解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
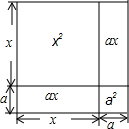 边长为(x+a)的正方形如图所示,则这个正方形的面积不能表示为( )
边长为(x+a)的正方形如图所示,则这个正方形的面积不能表示为( )| A. | (x+a)(x+a) | B. | x2+a2+2ax | C. | 4(x+a) | D. | (x+a)a+(x+a)x |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
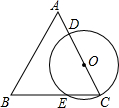 如图,△ABC是等边三角形,点O在边AC上(不与A,C重合),以点O为圆心,以OC为半径的圆分别与AC、BC相交于点D、E,若OC=1,则$\widehat{DE}$的长是$\frac{2π}{3}$(结果保留π).
如图,△ABC是等边三角形,点O在边AC上(不与A,C重合),以点O为圆心,以OC为半径的圆分别与AC、BC相交于点D、E,若OC=1,则$\widehat{DE}$的长是$\frac{2π}{3}$(结果保留π).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
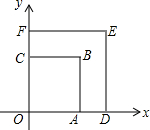 如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为2:3,点B、E在第一象限,若点A的坐标为(1,0),则点E的坐标是( )
如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为2:3,点B、E在第一象限,若点A的坐标为(1,0),则点E的坐标是( )| A. | ($\sqrt{2},0$) | B. | ($\frac{3}{2},\frac{3}{2}$) | C. | ($\sqrt{2},\sqrt{2}$) | D. | (2,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com