
如图,已知△ABC是等腰直角三角形,CD是斜边AB的中线,△ADC绕点D旋转一定角度得到△A'DC',A'D交AC于点E,DC'交BC于点F,连接EF,若
 ,则
,则
 = .
= .



 【考点】旋转的性质;平行线的判定;全等三角形的判定与性质;等腰直角三角形;平行线分线段成比例.
【考点】旋转的性质;平行线的判定;全等三角形的判定与性质;等腰直角三角形;平行线分线段成比例.
【专题】压轴题.
【分析】根据等腰直角三角形的性质及旋转的性质,运用“ASA”证明△ADE≌△CDF,得DE=DF.则有DE:DA′=DF:DC′,得EF∥A′C′.根据相似三角形性质求解.
【解答】解:∵△ABC是等腰直角三角形,CD是斜边AB的中线,
∴CD⊥AB,CD=AD,∠A=∠BCD=45°.
又∵∠ADE=90°﹣∠CDE=∠CDF,
∴△ADE≌△CDF (ASA)
∴DE=DF.
∵DA=DA′,DC=DC′,
∴DE:DA′=DF:DC′,
∴EF∥A′C′.
∴△DEF∽△DA′C′,
∴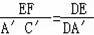
 .
.
∵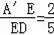
 ,则
,则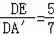
 ,
,
∴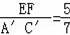
 .
.
故答案为
 .
.
【点评】此题考查等腰三角形性质、旋转的性质、全等三角形的判定与性质及平行线的判定和性质等知识点,综合性较强.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
平面直角坐标系xOy中,点A、B分别在函数y1=
 (x>0)与y2=﹣
(x>0)与y2=﹣
 (x<0)的图象上,A、B的横坐标分别为
(x<0)的图象上,A、B的横坐标分别为
a、b.


(1)若AB∥x轴,求△OAB的面积;
(2)若△OAB是以AB为底边的等腰三角形,且a+b≠0,求ab的值;
(3)作边长为3的正方形ACDE,使AC∥x轴,点D在点A的左上方,那么,对大于或等于4的任意实数a,CD边与函数y1=
 (x>0)的图象都有交点,请说明理由.
(x>0)的图象都有交点,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在▱ABCD中,对角线AC、BD相交成的锐角为α,若AC=a,BD=b,则▱ABCD的面积是( )


A.
 absinα B.absinα C.abcosα D.
absinα B.absinα C.abcosα D.
 abcosα
abcosα
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com