Question

【题目】已知：如图，在矩形ABCD中，M，N分别是边AD，BC的中点，E，F分别是线段BM，CM的中点．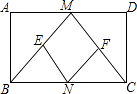
（1）求证：△ABM≌△DCM；
（2）判断四边形MENF是什么特殊四边形，并证明你的结论；
（3）当AD：AB=时，四边形MENF是正方形（只写结论，不需证明）．

Answer 1

【答案】
（1）证明：∵四边形ABCD是矩形，

∴AB=CD，∠A=∠D=90°，

又∵M是AD的中点，

∴AM=DM．

在△ABM和△DCM中，

，

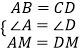∴△ABM≌△DCM（SAS）

（2）解：四边形MENF是菱形．

证明如下：

∵E，F，N分别是BM，CM，CB的中点，

∴NE∥MF，NE=MF．

∴四边形MENF是平行四边形．

由（1），得BM=CM，∴ME=MF．

∴四边形MENF是菱形

（3）2：1
【解析】（3）解： 当AD：AB=2：1时，四边形MENF是正方形．理由：
∵M为AD中点，
∴AD=2AM．
∵AD：AB=2：1，
∴AM=AB．
∵∠A=90，
∴∠ABM=∠AMB=45°．
同理∠DMC=45°，
∴∠EMF=180°﹣45°﹣45°=90°．
∵四边形MENF是菱形，
∴菱形MENF是正方形．
故答案为：2：1．
（1）根据矩形的性质可得AB=CD，∠A=∠D=90°，再根据M是AD的中点，可得AM=DM，然后再利用SAS证明△ABM≌△DCM；（2）四边形MENF是菱形．首先根据中位线的性质可证明NE∥MF，NE=MF，可得四边形MENF是平行四边形，再根据△ABM≌△DCM可得BM=CM进而得ME=MF，从而得到四边形MENF是菱形；（3）当AD：AB=2：1时，四边形MENF是正方形，证明∠EMF=90°根据有一个角为直角的菱形是正方形得到结论．