
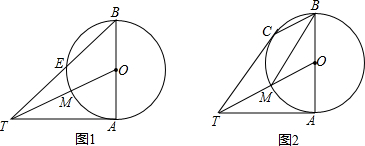
分析 (1)作OF⊥BT于F,根据等腰直角三角形的性质得出BF=EF=OF,再利用三角函数解答即可;
(2)根据切线的性质和平行线分线段成比例定理进行解答即可.
解答 解:(1)作OF⊥BT于F,则BF=EF=OF,
∴sin∠BTO=$\frac{OF}{OT}$=$\frac{\frac{1}{2}BE}{OT}$=$\frac{BE}{2OT}$
(2)∵BC∥OT,则∠CBM=∠BMO=∠ABM,作MN⊥AB于N,
∴tan∠AOT=$\frac{AT}{OA}$=2,
∴$\frac{MN}{ON}$=2,设ON=x,MN=2x,则OM=$\sqrt{5}$x=OB,
∴BN=($\sqrt{5}$+1)x,
∴tan∠CBM=tan∠ABM=$\frac{MN}{BN}$=$\frac{2x}{(\sqrt{5}+1)x}$=$\frac{\sqrt{5}-1}{2}$.
点评 本题考查的是切线的判定和平行线分线段成比例定理的应用,掌握经过半径的外端且垂直于这条半径的直线是圆的切线、灵活运用平行线分线段成比例定理是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 12 | C. | $\frac{1}{3}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
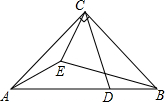 如图,在△ABC中,∠ACB=90°,AC=BC,点D在AB上,AD=9,BD=3,EA=EC,∠ECD=45°,则BE的长为$\frac{3\sqrt{26}}{2}$.
如图,在△ABC中,∠ACB=90°,AC=BC,点D在AB上,AD=9,BD=3,EA=EC,∠ECD=45°,则BE的长为$\frac{3\sqrt{26}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
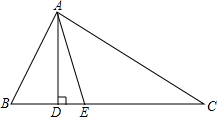 如图,△ABC中,AD⊥BC于D,AE平分∠BAC交BC边于点E,∠C=2∠DAE,AC=11,AB=6,则CE=$\frac{55}{6}$.
如图,△ABC中,AD⊥BC于D,AE平分∠BAC交BC边于点E,∠C=2∠DAE,AC=11,AB=6,则CE=$\frac{55}{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 购买数量(贴) | 单价(元/贴) |
| 不超过10贴(包含10贴) | 9 |
| 超过10贴不超过m贴的部分(15≤m≤30) | 8 |
| 超过m贴的部分 | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com