
【题目】某校积极推行“互动生成的学本课堂”卓有成效,“小组合作学习”深入人心,九年级某学习小组在操作实践过程中发现了一个有趣的问题:将直尺和三角板(三角板足够大)按如图所示的方式摆放在平面直角坐标系中,直尺的左侧边CD在直线x=4上,在保证直角三角板其中一条直角边始终过点A(0,4),同时使得直角顶点E在CD上滑动,三角板的另一直角边与x轴交于点B,当点E从点C(4,5)滑动到点D(4,0)的过程中,点B所经过的路径长为_____.

【答案】![]()
【解析】
过点A作AF⊥CD于F,分点E在点F上方和点F下方两种情况讨论,通过相似三角形的性质和二次函数的性质可求解.
解:如图,过点A作AF⊥CD于F,则AF=4,CF=1,
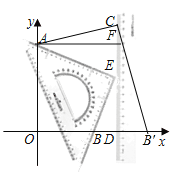
当点E与点C重合时,三角板与x轴交于点B',
∵∠ACB'=90°,AF⊥CD,
∴∠ACF+∠B'CD=90°,∠CAF+∠ACF=90°,
∴∠CAF=∠B'CD,且∠AFC=∠B'DC=90°,
∴△ACF∽△CB'D,
∴![]() ,
,
∴![]() ,
,
∴B'D=![]() ,
,
∴点E从点C到点F,点B所经过的路径为![]() ,
,
当点E从点F到点D时,∵∠AEF+∠BED=90°,∠AEF+∠EAF=90°,
∴∠BED=∠EAF,
又∵∠AFE=∠EDB=90°,
∴△AEF∽△EBD,
∴![]() ,
,
∴![]()
∴BD=![]() ,
,
∴当EF=2时,BD有最大值为1,
∴点E从点F到点D,点B所经过的路径为2,
∴点B所经过的路径长=2+![]() =
=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
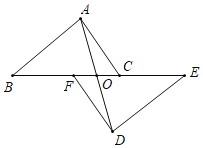
【题目】如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,AD交BE于O.
(1)求证:△ABC≌△DEF;
(2)求证:AD与BE互相平分;
(3)若BF=5,FC=4,直接写出EO的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条笔直的公路![]() 穿过草原,公路边有一卫生站
穿过草原,公路边有一卫生站![]() 距公路
距公路![]() 的地方有一居民点
的地方有一居民点![]() ,
,![]() 、
、![]() 之间的距离为
之间的距离为![]() .一天某司机驾车从卫生站送一批急救药品到居民点.已知汽车在公路上行驶的最快速度是
.一天某司机驾车从卫生站送一批急救药品到居民点.已知汽车在公路上行驶的最快速度是![]() ,在草地上行驶的最快速度是
,在草地上行驶的最快速度是![]() .问司机应在公路上行驶多少千米?全部所用的行车时间最短?最短时间为多少?
.问司机应在公路上行驶多少千米?全部所用的行车时间最短?最短时间为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在菱形ABCD中,动点P从点B出发,沿折线B→C→D→B运动.设点P经过的路程为x,△ABP的面积为y.把y看作x的函数,函数的图象如图②所示,则图②中的b等于( )

A. ![]() B.
B. ![]() C. 5D. 4
C. 5D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种货车,3辆大货车与4辆小货车一次可以运货18吨,2辆大货车与6辆小货车一次可以运货17吨.
(1)请问1辆大货车和1辆小货车一次可以分别运货多少吨?
(2)目前有33吨货物需要运输,货运公司拟安排大小货车共计10辆,全部货物一次运完,其中每辆大货车一次运费花费130元,每辆小货车一次运货花费100元,请问货运公司应如何安排车辆最节省费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴交于点B,与y轴交于点C,抛物线
与x轴交于点B,与y轴交于点C,抛物线![]() 经过B、C两点,且与x轴交于另一点A.
经过B、C两点,且与x轴交于另一点A.
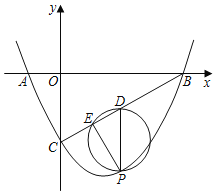
(1)求抛物线的解析式.
(2)点P是线段BC下方的抛物线上的动点(不与点B、C重合),过P作PD∥y轴交BC于点D,以PD为直径的圆交BC于另一点E,求DE的最大值及此时点P的坐标;
(3)当(2)中的DE取最大值时,将△PDE绕点D旋转,当点P落在坐标轴上时,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
情景再现
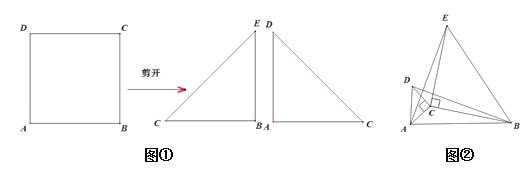
我们动手操作:把正方形ABCD,从对角线剪开就分剪出两个等腰直角三角形,把其中一个等腰三角形与正方形ABCD重新组合在一起,图形变得丰富起来,当图形旋转时问题也随旋转应运而生.
如图①把正方形ABCD沿对角线剪开,得两个等腰直角三角形△ACD和△BCE,
(1)问题呈现
我们把剪下的两个三角形一个放大另一个缩小拼成如图②所示
①点P是一动点,若AB=3,PA=1,当点P位于_ __时,线段PB的值最小;若AB=3,PA=5,当点P位于__ _时,线段PB有最大值.PB的最大值和最小值分别是______.
②直接写出线段AE与DB的关系是_ ________.
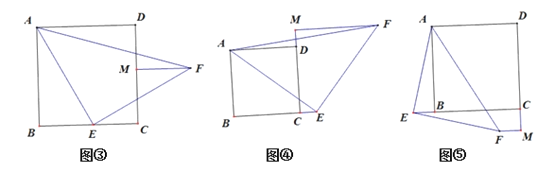
(2)我们把剪下的其中一个三角形放大与正方形组合如图③所示,点E在直线BC上,FM⊥CD交直线CD于M.
①当点E在BC上时,通过观察、思考易证:AD=MF+CE;
②当点E在BC的延长线时,如图④所示;
当点E在CB的延长线上时,如图⑤所示,
线段AD、MF、CE具有怎样的数量关系?写出你的猜想,并选择图④或图⑤证明你的猜想.
问题拓展
(3)连接EM,当![]() =8,
=8,![]() =50,其他条件不变,直接写出线段CE的长_______.
=50,其他条件不变,直接写出线段CE的长_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在由边长为 1 个单位长度的小正方形组成的网格中,建立平面直角坐标系 A(1,7), B(6,3), C(2,3) .
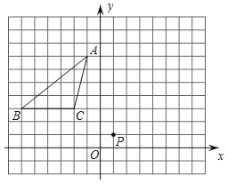
(1)将ABC 绕格点 P(1,1) 顺时针旋转90,得到△ ABC, 画出△ ABC,并写出下列各点坐标: A( , ), B( , ), C( , );
(2)找格点 M ,连CM ,使CM AB ,则点 M 的坐标为( );
(3)找格点 N ,连 BN ,使 BN AC ,则点 N 的坐标为( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com