
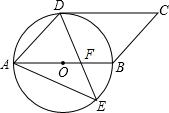
 如图,四边形ABCD是平行四边形,以AB为直径的圆O经过点D,E是⊙O上一点,且∠AED=45°,DE交直径AB于点F.
如图,四边形ABCD是平行四边形,以AB为直径的圆O经过点D,E是⊙O上一点,且∠AED=45°,DE交直径AB于点F.分析 (1)连结OD,根据圆周角定理得∠AOD=2∠AED=90°,则OD⊥AB,再根据平行四边形的性质得AB∥DC,所以OD⊥DC,则根据切线的判定定理得到CD为⊙O的切线;
(2)作AH⊥EF于H,连结BE,由圆周角定理得出∠AEB=90°,∠ADE=∠ABE,由三角函数求出AB=4$\sqrt{2}$,得出OA=2$\sqrt{2}$,求出AH=EH=$\frac{\sqrt{2}}{2}$AE=$\sqrt{2}$,由△AHF∽△DOF,得出$\frac{AH}{DO}=\frac{HF}{OF}$,得出OF=2HF,在Rt△AHF中,由勾股定理求出HF,得出OF,EF=EH+HF,即可得出结果.
解答 解:(1)CD与⊙O相切.理由如下: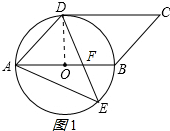
连结OD,如图1所示,
∵∠AOD=2∠AED=2×45°=90°,
∴OD⊥AB,
∵四边形ABCD是平行四边形,
∴AB∥DC,
∴OD⊥DC,
∴CD为⊙O的切线;
(2)作AH⊥EF于H,连结BE,如图2所示,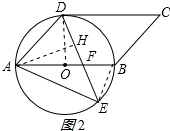
∵AB为直径,
∴∠AEB=90°,
∵∠ADE=∠ABE,
∴sin∠ADE=sin∠ABE=$\frac{AE}{AB}$=$\frac{\sqrt{2}}{4}$,而AE=2,
∴AB=4$\sqrt{2}$,
∴OA=2$\sqrt{2}$,
在Rt△AEH中,∠AEH=45°,
∴AH=EH=$\frac{\sqrt{2}}{2}$AE=$\sqrt{2}$,
∵△AHF∽△DOF,
∴$\frac{AH}{DO}=\frac{HF}{OF}$,
即$\frac{HF}{OF}=\frac{\sqrt{2}}{2\sqrt{2}}$,
∴OF=2HF,
∴AF=OA-OF=OA-2HF,
在Rt△AHF中,AH2+FH2=AF2,
∴($\sqrt{2}$)2+HF2=(2$\sqrt{2}$-2HF)2,
解得:HF=$\frac{4\sqrt{2}-\sqrt{14}}{3}$或$\frac{4\sqrt{2}+\sqrt{14}}{3}$(舍去),
∴OF=2HF=$\frac{8\sqrt{2}-2\sqrt{14}}{3}$,
∴EF=EH+HF=$\sqrt{2}$+$\frac{4\sqrt{2}-\sqrt{14}}{3}$=$\frac{7\sqrt{2}-\sqrt{14}}{3}$.
点评 本题考查了切线的判定定理、平行四边形的性质、勾股定理、相似三角形的判定与性质和解直角三角形等知识;本题综合性强,有一定难度.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
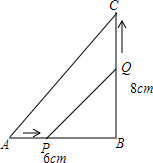 如图,在△ABC中,∠B=90°,点P从A点开始沿AB边向B以1厘米/秒的速度移动,点Q从B点开始沿BC边向点C以2厘米/秒的速度移动.如果P、Q分别分别从A、B两点同时出发,经过几秒钟,△PBQ的面积等于8厘米2?
如图,在△ABC中,∠B=90°,点P从A点开始沿AB边向B以1厘米/秒的速度移动,点Q从B点开始沿BC边向点C以2厘米/秒的速度移动.如果P、Q分别分别从A、B两点同时出发,经过几秒钟,△PBQ的面积等于8厘米2?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
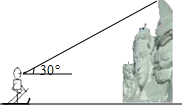 长春瓦萨国际滑雪节制作了很多雪雕,一名滑雪运动员的眼部距地面1.8米,他站在一座雪雕前观测这座雪雕顶部的仰角为30°,此时他的眼部到雪雕顶部的距离为4米,如图,那么雪雕的高度为6米.
长春瓦萨国际滑雪节制作了很多雪雕,一名滑雪运动员的眼部距地面1.8米,他站在一座雪雕前观测这座雪雕顶部的仰角为30°,此时他的眼部到雪雕顶部的距离为4米,如图,那么雪雕的高度为6米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系xOy中,梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,过点A的双曲线y=$\frac{k}{x}$的一支在第一象限交梯形对角线OC于点D,交边BC于点E.若点C的坐标为(2,2),则阴影部分面积S最小值为$\frac{3}{2}$.
如图,在平面直角坐标系xOy中,梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,过点A的双曲线y=$\frac{k}{x}$的一支在第一象限交梯形对角线OC于点D,交边BC于点E.若点C的坐标为(2,2),则阴影部分面积S最小值为$\frac{3}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com