
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D为AC边上的动点,点D从点C出发,沿边CA往A运动,当运动到点A时停止,若设点D运动的时间为t秒,点D运动的速度为每秒1个单位长度
(1)当t=2时,CD=______,AD=______;(请直接写出答案)
(2)当△CBD是直角三角形时,t=______;(请直接写出答案)
(3)求当t为何值时,△CBD是等腰三角形?并说明理由.

【答案】(1)CD=2,AD=8;(2) t=3.6或10秒;(3)t=5秒或6秒或7.2秒时,△CBD是等腰三角形,理由见解析
【解析】
(1)根据CD=速度×时间列式计算即可得解,利用勾股定理列式求出AC,再根据AD=AC-CD代入数据进行计算即可得解;
(2)分①∠CDB=90°时,利用△ABC的面积列式计算即可求出BD,然后利用勾股定理列式求解得到CD,再根据时间=路程÷速度计算;②∠CBD=90°时,点D和点A重合,然后根据时间=路程÷速度计算即可得解;
(3)分①CD=BD时,过点D作DE⊥BC于E,根据等腰三角形三线合一的性质可得CE=BE,从而得到CD=AD;②CD=BC时,CD=6;③BD=BC时,过点B作BF⊥AC于F,根据等腰三角形三线合一的性质可得CD=2CF,再由(2)的结论解答.
(1)t=2时,CD=2×1=2,
∵∠ABC=90°,AB=8,BC=6,
∴AC=![]() =10,
=10,
AD=AC-CD=10-2=8;
(2)①∠CDB=90°时,S△ABC=![]() ACBD=
ACBD=![]() ABBC,
ABBC,
即![]() ×10BD=
×10BD=![]() ×8×6,
×8×6,
解得BD=4.8,
∴CD=![]() =3.6,
=3.6,
t=3.6÷1=3.6秒;
②∠CBD=90°时,点D和点A重合,
t=10÷1=10秒,
综上所述,t=3.6或10秒;
故答案为:(1)2,8;(2)3.6或10秒;
(3)①CD=BD时,如图1,过点D作DE⊥BC于E,
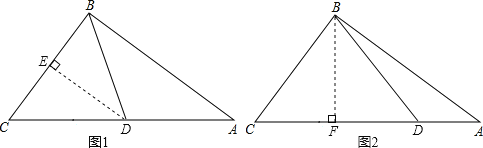
则CE=BE,
∴CD=AD=![]() AC=
AC=![]() ×10=5,
×10=5,
t=5÷1=5;
②CD=BC时,CD=6,t=6÷1=6;
③BD=BC时,如图2,过点B作BF⊥AC于F,
则CF=3.6,
CD=2CF=3.6×2=7.2,
∴t=7.2÷1=7.2,
综上所述,t=5秒或6秒或7.2秒时,△CBD是等腰三角形.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】星光橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:
进价(元/台) | 售价(元/台) | |
电饭煲 | 200 | 250 |
电压锅 | 160 | 200 |
(1)一季度,橱具店购进这两种电器共30台,用去了5600元,并且全部售完,问橱具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50台,且电饭煲的数量不少于电压锅的 ![]() ,问橱具店有哪几种进货方案?并说明理由;
,问橱具店有哪几种进货方案?并说明理由;
(3)在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
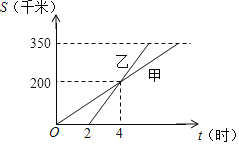
【题目】如图,甲、乙两人利用不同的交通工具,沿同一路线从A地出发到距离A地350千米的B地办事,甲先出发,乙后出发,甲、乙两人距A地的路程和时间的关系如图所示,根据图示提供的信息解答:
![]() 乙比甲晚______小时出发;乙出发______小时后追上甲;
乙比甲晚______小时出发;乙出发______小时后追上甲;
![]() 分别求甲、乙两人离开A地的路程s关于t的函数关系式;
分别求甲、乙两人离开A地的路程s关于t的函数关系式;
![]() 求乙比甲早几小时到达B地?
求乙比甲早几小时到达B地?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行“行动起来,对抗雾霾”为主题的植树活动,某街道积极响应,决定对该街道进行绿化改造,共购进甲、乙两种树共500棵,已知甲树每棵800元,乙树每棵1200元.
(1)若购买两种树总金额为560000元,求甲、乙两种树各购买了多少棵?
(2)若购买甲树的金额不少于购买乙树的金额,至少应购买甲树多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中,已知![]() ,其中
,其中![]() 满足
满足![]() .
.
(1)填空:![]() = _____ ,
= _____ ,![]() = _____ ;
= _____ ;
(2)如果在第三象限内一点![]() ,请用含
,请用含![]() 的式子表示⊿
的式子表示⊿![]() 的面积;
的面积;
(3)若⑵条件下,当![]() 时,在坐标轴上一点
时,在坐标轴上一点![]() ,使得⊿
,使得⊿![]() 的面积与⊿
的面积与⊿![]() 的面积相等,请求出点
的面积相等,请求出点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学在全校学生中开展了“地球﹣我们的家园”为主题的环保征文比赛,评选出一、二、三等奖和优秀奖,根据奖项的情况绘制成如图所示的两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)该校获奖的总人数为 , 并把条形统计图补充完整;
(2)求在扇形统计图中表示“二等奖”的扇形的圆心角的度数;
(3)获得一等奖的4名学生中有3男1女,现打算从中随机选出2名学生参加颁奖活动,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作探究:已知在纸面上有一数轴(如图所示),
![]()
(1)折叠纸面,使表示的点1与-1重合,则-2表示的点与 表示的点重合;
(2)折叠纸面,使-1表示的点与3表示的点重合,回答以下问题:
① 5表示的点与数 表示的点重合;
②![]() 表示的点与数 表示的点重合;
表示的点与数 表示的点重合;
③若数轴上A、B两点之间距离为9(A在B的左侧),且A、B两点经折叠后重合,此时点A表示的数是 、点B表示的数是 .
(3)已知在数轴上点A表示的数是a,点A移动4个单位,此时点A表示的数和a是互为相反数,求a的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com