
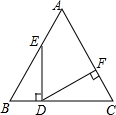
 如图,在等边△ABC中,点D为BC边上的点,DE⊥BC交AB于E,DF⊥AC于F,则∠EDF的度数为60°.
如图,在等边△ABC中,点D为BC边上的点,DE⊥BC交AB于E,DF⊥AC于F,则∠EDF的度数为60°. 分析 先根据等边三角形的性质得出∠A=∠B=60°,再由DE⊥BC交AB于E,DF⊥AC于F得出∠BDE=∠AFD=90°,根据三角形外角的性质求出∠AED的度数,由四边形内角和定理即可得出结论.
解答 解:∵△ABC是等边三角形,
∴∠A=∠B=60°.
∵DE⊥BC交AB于E,DF⊥AC于F,
∴∠BDE=∠AFD=90°.
∵∠AED是△BDE的外角,
∴∠AED=∠B+∠BDE=60°+90°=150°,
∴∠EDF=180°-∠A-∠AED-∠AFD=360°-60°-150°-90°=60°.
故答案为:60°.
点评 本题考查的是等边三角形,三角形内角和定理及直角三角形的性质,熟练掌握等边三角形的性质是解题的关键.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (8+t)℃ | B. | (8-t)℃ | C. | (t-8)℃ | D. | (-t-8)℃ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 近年来,合肥“大建设”已经取得了令人瞩目的成就,今年合肥市继续重点实施综合交通、园林绿化和环境综合整治等八大类工程.如图是某建筑工地搭建的临时帐篷的横截面,其上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成,最大高度为6米,底部宽度为12米,OE=3米,如果还要搭建一个矩形“支撑架”,使C、D点在抛物线上,A、B点在地面OM上,则这个“支撑架”总长L(L=AD+DC+CB)的最大值是多少?
近年来,合肥“大建设”已经取得了令人瞩目的成就,今年合肥市继续重点实施综合交通、园林绿化和环境综合整治等八大类工程.如图是某建筑工地搭建的临时帐篷的横截面,其上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成,最大高度为6米,底部宽度为12米,OE=3米,如果还要搭建一个矩形“支撑架”,使C、D点在抛物线上,A、B点在地面OM上,则这个“支撑架”总长L(L=AD+DC+CB)的最大值是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则sin∠ECB为( )
如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则sin∠ECB为( )| A. | $\frac{3}{5}$ | B. | $\frac{3\sqrt{13}}{13}$ | C. | $\frac{2}{3}$ | D. | $\frac{2\sqrt{13}}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 按要求用尺规作图,保留作图痕迹,不写作法
按要求用尺规作图,保留作图痕迹,不写作法查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>$\frac{1}{2}$ | B. | $\frac{1}{2}$≤x<5 | C. | $\frac{1}{2}$<x<7 | D. | $\frac{1}{2}$<x≤7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com