
【题目】如图,点F在正方形ABCD的边BC上,E在AB的延长线上,FB=EB,AF的延长线交CE于G,则∠AGC的度数是___________.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,若∠DAB的角平分线AE交CD于E,连接BE,且BE边平分∠ABC,则以下命题不正确的个数是①BC+AD=AB;②E为CD中点;③∠AEB=90°;④S△ABE=![]() S四边形ABCD;⑤BC=CE.( )
S四边形ABCD;⑤BC=CE.( )

A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D、E分别在△ACD的边AB和AC上,已知DE∥BC,DE=DB.
(1)请用直尺和圆规在图中画出点D和点E(保留作图痕迹,不要求写作法),并证明所作的线段DE是符合题目要求的;
(2)若AB=7,BC=3,请求出DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是它的角平分线,G是AD上的一点,BG,CG分别平分∠ABC,∠ACB,GH⊥BC,垂足为H,

求证:(1)∠BGC=90°+![]() ∠BAC;
∠BAC;
(2)∠1=∠2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:矩形ABCD中,AB=4,BC=3,点M、N分别在边AB、CD上,直线MN交矩形对角线 AC于点E,将△AME沿直线MN翻折,点A落在点P处,且点P在射线CB上.
(1)如图1,当EP⊥BC时,求CN的长;
(2) 如图2,当EP⊥AC时,求AM的长;
(3) 请写出线段CP的长的取值范围,及当CP的长最大时MN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
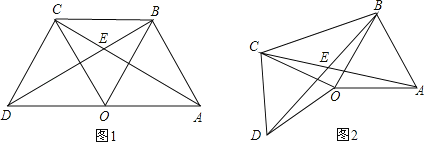
【题目】(1)如图1,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连接AC和BD,相交于点E,连接BC.求∠AEB的大小;
(2)如图2,△OAB固定不动,保持△OCD的形状和大小不变,将△OCD绕点O旋转(△OAB和△OCD不能重叠),求∠AEB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小莉和她爸爸两人沿长江边扬子江步道匀速跑步,他们从渡江胜利纪念馆同时出发,终点是绿博园.已知小莉比她爸爸每步少跑![]() ,两人的运动手环记录时间和步数如下:
,两人的运动手环记录时间和步数如下:
出发 | 途中 | 结束 | |
时间 |
|
|
|
小莉的步数 | 1308 | 3183 | 8808 |
出发 | 途中 | 结束 | |
时间 |
|
|
|
爸爸的步数 | 2168 | 4168 |
|
(1)表格中![]() 表示的结束时间为 ,
表示的结束时间为 ,![]() ;
;
(2)小莉和她爸爸两人每步分别跑多少米?
(3)渡江胜利纪念馆到绿博园的路程是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).
(1)请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.
,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】铜仁某校高中一年级组建篮球队,对甲、乙两名备选同学进行定位投篮测试,每次投10个球,共投10次.甲、乙两名同学测试情况如图所示:

![]() 根据图6提供的信息填写下表:
根据图6提供的信息填写下表:
平均数 | 众数 | 方差 | |
甲 |
| ||
乙 |
|
![]() 如果你是高一学生会文体委员,会选择哪名同学进入篮球队?请说明理由.
如果你是高一学生会文体委员,会选择哪名同学进入篮球队?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com