
【题目】如图,以等边△ABC的边BC为直径作⊙O,分别交AB、AC于点D、E,过点D作DF⊥AC交AC于点F.
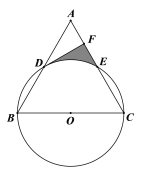
(1)求证:DF是⊙O的切线;
(2)若等边△ABC的边长为8,求图中阴影部分的面积.
【答案】(1)见解析;(2) ![]()
![]()
【解析】
(1)连接![]() 、
、![]() ,先利用等腰三角形的性质证
,先利用等腰三角形的性质证![]() ,再证
,再证![]() 为
为![]() 的中位线得
的中位线得![]() ,根据
,根据![]() 可得;
可得;
(2)连接![]() 、作
、作![]() ,求出
,求出![]() 、
、![]() 的长及
的长及![]() 的度数,根据阴影部分面积
的度数,根据阴影部分面积![]() 计算可得.
计算可得.
(1)证明:连接OD、CD
∵DF⊥AC
∴∠AFD=90°.
∵BC是⊙O的直径
∴∠CDB=90°
∴CD⊥AB.
又∵△ABC是等边三角形
∴BD=AD
∵OB=OC
∴OD是△ABC的中位线
∴OD//AC
∴∠FDO=∠AFD=90°
∴OD⊥DF
∴DF是⊙O的切线
(2)连接OE,作OG⊥AC于G则∠OGF=∠GFD=∠FDO=90°
∴四边形ODFG是矩形
∴OD=FG=![]()
又∵OB=OD=OE=OC,∠B=∠ACB=60°
∴△OBD、△OCE是等边三角形
∴∠BOD=∠COE=60°,CE=OC=4.
∴∠DOE=60°,EG=![]()
∴![]()
![]()
∴![]()
![]()



科目:初中数学 来源: 题型:
【题目】如图,抛物线的图像经过点A(4,4),B(5,0)和原点O,点P为抛物线上的一个动点,过点P作x轴的垂线,垂足为D(m,0)(m>0),并与直线OA交于点C.
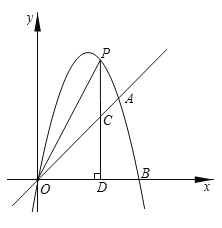
(1)求出抛物线的函数表达式;
(2)连接OP,当S△OPC=![]() S△OCD时,求出此时的点P坐标;
S△OCD时,求出此时的点P坐标;
(3)在直线OA上取一点M,使得以P、C、M为顶点的三角形与△OCD全等,求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现:(1)如图1,在等腰直角三角形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 上一点,将射线
上一点,将射线![]() 顺时针旋转
顺时针旋转![]() 交
交![]() 于点
于点![]() ,则
,则![]() 与
与![]() 的数量关系为____;
的数量关系为____;
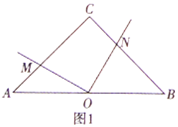
问题探究:(2)如图2,在等腰三角形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 上一点,将射线
上一点,将射线![]() 顺时针旋转
顺时针旋转![]() 交
交![]() 于点
于点![]() ,则
,则![]() 与
与![]() 的数量关系是否改变,请说明理由;
的数量关系是否改变,请说明理由;
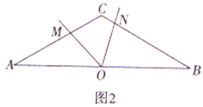
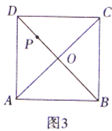
问题解决:(3)如图3,点![]() 为正方形
为正方形![]() 对角线的交点,点
对角线的交点,点![]() 为
为![]() 的中点,点
的中点,点![]() 为直线
为直线![]() 上一点,将射线
上一点,将射线![]() 顺时针旋转
顺时针旋转![]() 交直线
交直线![]() 于点
于点![]() ,若
,若![]() ,当
,当![]() 面积为
面积为![]() 时,直接写出线段
时,直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
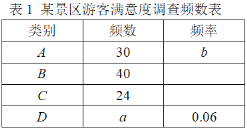
【题目】为了解游客对某景区的满意度,特对游客采取随机抽样的方式进行问卷调查,调查的结果分为A,B,C,D四类,其含意依次表示为“非常满意”、“比较满意”、“基本满意”和“不太满意”,划分类别后的数据整理如表1(不完整).
(1)求表中的数据a和b.
(2)如果根据表中频数画扇形统计图,那么类别为B的频数所对应的扇形圆心角是几度?
(3)已知该景区每日游客限流3000名,估计一天的游客中类别C的游客人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长分别为10cm和4cm的矩形纸片沿着虚线剪成两个全等的梯形纸片.裁剪线与矩形较长边所夹的锐角是45°,则梯形纸片中较短的底边长为( )
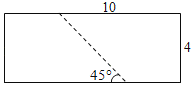
A.2cmB.2.5cmC.3cmD.3.5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
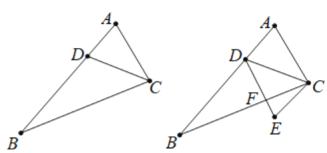
【题目】如图1,在△ABC中,D是AB上一点,已知AC=10,AC2=AD·AB.
(1)证明△ACD∽△ABC.
(2)如图2,过点C作CE∥AB,且CE=6,连结DE交BC于点F;
①若四边形ADEC是平行四边形,求![]() 的值;
的值;
②设AD=x,![]() =y,求y关于x的函数表达式.
=y,求y关于x的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
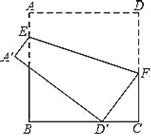
【题目】如图,正方形![]() 的边长是9,点
的边长是9,点![]() 是
是![]() 边上的一个动点,点
边上的一个动点,点![]() 是
是![]() 边上一点,
边上一点,![]() ,连接
,连接![]() ,把正方形
,把正方形![]() 沿
沿![]() 折叠,使点
折叠,使点![]() ,
,![]() 分别落在点
分别落在点![]() ,
,![]() 处,当点
处,当点![]() 落在线段
落在线段![]() 上时,线段
上时,线段![]() 的长为__________.
的长为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com