
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,分别交直线
,分别交直线![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
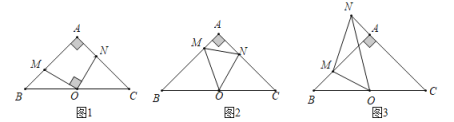
(1)如图1,当![]() 时,求证:
时,求证:![]() ;
;
(2)如图2,当![]() 时,线段
时,线段![]() 、
、![]() 、
、![]() 之间有何数量关系,证明你的结论;
之间有何数量关系,证明你的结论;
(3)如图3,当![]() 时,旋转
时,旋转![]() ,问线段之间
,问线段之间![]() 、
、![]() 、
、![]() 有何数量关系?证明你的结论.
有何数量关系?证明你的结论.
【答案】(1)见解析;(2)![]() ,证明见解析;(3)
,证明见解析;(3)![]() ,证明见解析
,证明见解析
【解析】
(1)根据等腰直角三角形的性质可得![]() ,
,![]() ,
,![]() ,然后利用ASA证出
,然后利用ASA证出![]() ,从而证出结论;
,从而证出结论;
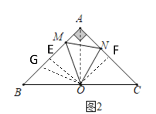
(2)过![]() 作
作![]() ,
,![]() ,连接AO,证出
,连接AO,证出![]() ,AO平分∠BAC,
,AO平分∠BAC,![]() ,从而得出OE=OF,BE=OE,将△ONF逆时针旋转,使OF和OE重合,点N落在点G处,利用SAS即可证出△MOG≌△MON,得出MN =GM,再结合正方形的性质和等量代换即可得出结论;
,从而得出OE=OF,BE=OE,将△ONF逆时针旋转,使OF和OE重合,点N落在点G处,利用SAS即可证出△MOG≌△MON,得出MN =GM,再结合正方形的性质和等量代换即可得出结论;
(3)在![]() 上截取
上截取![]() ,连接
,连接![]() ,先利用SAS证出
,先利用SAS证出![]() ,从而得出
,从而得出![]() ,
,![]() ,再利用SAS证出
,再利用SAS证出![]() ,最后利用等量代换即可得出结论.
,最后利用等量代换即可得出结论.
证明:(1)∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]()
∵![]() ,
,
∴∠AOM+∠AON=90°,∠CON+∠AON=90°
∴![]()
在△AOM和△CON中
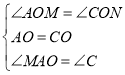
∴![]() ,
,
∴![]()
(2)![]() 、
、![]() 、
、![]() 之间的数量关系是:
之间的数量关系是:![]()
过![]() 作
作![]() ,
,![]() ,连接AO
,连接AO
∴四边形![]() 为矩形
为矩形
∵![]() ,
,![]() ,
,![]()
∴![]() ,AO平分∠BAC,
,AO平分∠BAC,![]()
∴OE=OF,BE=OE
∴四边形![]() 为正方形,
为正方形,
∵![]()
将△ONF逆时针旋转,使OF和OE重合,点N落在点G处
∴∠MOG=∠EOM+∠NOF=90°-∠MON=45°=![]() ,OG=ON,GE=FN
,OG=ON,GE=FN
在△MOG和△MON中
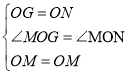
∴△MOG≌△MON
∴MN =GM=EM+GE=![]()
∴![]()
而![]()
∴![]()
(3)![]()
在![]() 上截取
上截取![]() ,连接
,连接![]()
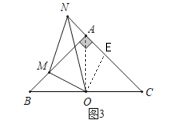
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
在△BOM和△AOE中
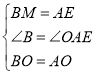
∴![]() ,
,
∴![]() ,
,![]()
∵![]() ,
,
∴![]()
即![]() ,
,
在△MON和△EON中
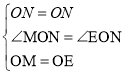
∴![]()
∴![]()


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() ,
,![]() ,直线
,直线![]() 与
与![]() 轴和
轴和![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,若抛物线
,若抛物线![]() 与直线
与直线![]() 有两个不同的交点,其中一个交点在线段
有两个不同的交点,其中一个交点在线段![]() 上(包含
上(包含![]() ,
,![]() 两个端点),另一个交点在线段
两个端点),另一个交点在线段![]() 上(包含
上(包含![]() ,
,![]() 两个端点),则
两个端点),则![]() 的取值范围是
的取值范围是

A. ![]() B.
B. ![]() 或
或![]() C.
C. ![]() D.
D. ![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列一组方程:①![]() ,②
,②![]() ,③
,③![]() ,…小明通过观察,发现了其中蕴含的规律,并顺利地求出了前三个方程的解第①个方程的解为
,…小明通过观察,发现了其中蕴含的规律,并顺利地求出了前三个方程的解第①个方程的解为![]() ;第②个方程的解为
;第②个方程的解为![]() ;第③个方程的解为
;第③个方程的解为![]() .若n为正整数,且关于x的方程
.若n为正整数,且关于x的方程![]() 的一个解是
的一个解是![]() ,则n的值等于____________.
,则n的值等于____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
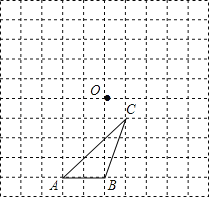
【题目】如图所示,△ABC与点O在10×10的网格中的位置如图所示
(1)画出△ABC绕点O逆时针旋转90°后的图形;
(2)画出△ABC绕点O逆时针旋转180°后的图形;
(3)若⊙M能盖住△ABC,则⊙M的半径最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在同一平面内,将△ABC绕A点逆时针旋转到△ADE的位置.若AC⊥DE,∠ABD=62°,则∠ACB的度数为( )

A.56°B.44°C.34°D.40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】慧秀中学在防“非典”知识竞赛中,评出一等奖4人,二等奖6人,三等奖20人,学校决定给所有获奖学生各发一份奖品,同一等次的奖品相同.
(1)若一等奖,二等奖、三等奖的奖品分别是喷壶、口罩和温度计,购买这三种奖品共计花费113元,其中购买喷壶的总钱数比购买口罩的总钱数多9元,而口罩的单价比温度计的单价多2元,求喷壶、口罩和温度计的单价各是多少元?
(2)若三种奖品的单价都是整数,且要求一等奖的单价是二等奖单价的2倍,二等奖的单价是三等奖单价的2倍,在总费用不少于90元而不足150元的前提下,购买一、二、三等奖奖品时它们的单价有几种情况,分别求出每种情况中一、二、三等奖奖品的单价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC.以AB为直径的⊙O分别与BC、AC相交于点D、E,连接AD.过点D作DF⊥AC,垂足为点F,
(1)求证:DF是⊙O的切线;
(2)若⊙O的半径为4,∠CDF=22.5°,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,为了改造小区环境,某小区决定要在一块一边靠墙(墙的最大可使用长度12m)的空地上建造一个矩形绿化带.除靠墙一边(AD)外,用长为32m的栅栏围成矩形ABCD.设绿化带宽AB为xm,面积为Sm2,
(1)求S与x的函数关系式,并直接写出x的取值范围;
(2)绿化带的面积能达到128m2吗?若能,请求出AB的长度;若不能,请说明理由;
(3)当x为何值时,满足条件的绿化带面积最大.

查看答案和解析>>
科目:初中数学 来源: 题型:
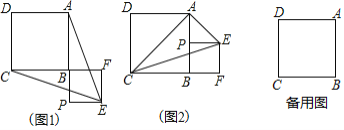
【题目】已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA、EC.
(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)若点P在线段AB上,如图2,当点P为AB的中点时,判断△ACE的形状,并说明理由;
(3)在(1)的条件下,将正方形ABCD固定,正方形BPEF绕点B旋转一周,设AB=4,BP=a,若在旋转过程中△ACE面积的最小值为4,请直接写出a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com