
����Ŀ��������ѧ�ڷ����ǵ���֪ʶ�����У�����һ�Ƚ�4�ˣ����Ƚ�6�ˣ����Ƚ�20�ˣ�ѧУ���������л�ѧ������һ�ݽ�Ʒ��ͬһ�ȴεĽ�Ʒ��ͬ��
(1)��һ�Ƚ������Ƚ������Ƚ��Ľ�Ʒ�ֱ�����������ֺ��¶ȼƣ����������ֽ�Ʒ���ƻ���113Ԫ�����й����������Ǯ���ȹ�����ֵ���Ǯ����9Ԫ�������ֵĵ��۱��¶ȼƵĵ��۶�2Ԫ������������ֺ��¶ȼƵĵ��۸��Ƕ���Ԫ��
(2)�����ֽ�Ʒ�ĵ��۶�����������Ҫ��һ�Ƚ��ĵ����Ƕ��Ƚ����۵�2�������Ƚ��ĵ��������Ƚ����۵�2�������ܷ��ò�����90Ԫ������150Ԫ��ǰ���£�����һ���������Ƚ���Ʒʱ���ǵĵ����м���������ֱ����ÿ�������һ���������Ƚ���Ʒ�ĵ��ۣ�
���𰸡���1����������ֺ��¶ȼƵĵ��۷ֱ���9Ԫ��4.5Ԫ��2.5Ԫ����2������һ���������Ƚ���Ʒʱ���ǵĵ����������������һ�������һ���������Ƚ���Ʒ�ĵ��۷ֱ���8Ԫ��4Ԫ��2Ԫ���ڶ��������һ���������Ƚ���Ʒ�ĵ��۷ֱ���12Ԫ��6Ԫ��3Ԫ��
��������
(1)�����������Ϳ��ֵĵ��۷ֱ���yԪ��zԪ��Ȼ����������г������飬���ɵó��𰸣�
(2)����������Ƚ���Ʒ�ĵ���ΪxԪ������Ƚ���Ʒ�ĵ���Ϊ2xԪ��һ�Ƚ���Ʒ�ĵ���Ϊ4xԪ���ٸ�������ò���ʽ�飺90��4��4x+6��2x+20x��150�����x��ȡֵ�ٴ���2x��4x���ɣ�
�⣺(1)������Ϳ��ֵĵ��۷ֱ���yԪ��zԪ��
�������⣬��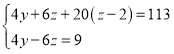 ��
��
���![]()
���ԣ�z��2��2.5
����������ֺ��¶ȼƵĵ��۷ֱ���9Ԫ��4.5Ԫ��2.5Ԫ��
(2)�����Ƚ���Ʒ�ĵ���ΪxԪ��
����Ƚ���Ʒ�ĵ���Ϊ2xԪ��һ�Ƚ���Ʒ�ĵ���Ϊ4xԪ��
�������⣬��90��4��4x+6��2x+20x��150
���![]() ��x��
��x��![]() ��
��
��Ϊ���ֽ�Ʒ�ĵ��۶�������������x��2����x��3��
��x��2ʱ��2x��4��4x��8����x��3ʱ��2x��6��4x��12��
�𣺹���һ���������Ƚ���Ʒʱ���ǵĵ����������������һ�������һ���������Ƚ���Ʒ�ĵ��۷ֱ���8Ԫ��4Ԫ��2Ԫ���ڶ��������һ���������Ƚ���Ʒ�ĵ��۷ֱ���12Ԫ��6Ԫ��3Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
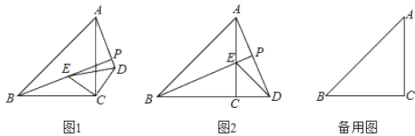
����Ŀ����ͼ1����ABC�͡�DEC��Ϊ���������Σ��ҡ�ACB=��DCE=90��������BE��AD�������߶����ڵ�ֱ�߽��ڵ�P.
��1���߶�BE��AD�к�������ϵ��λ�ù�ϵ����˵�����ɣ�
��2������֪BC=12��DC=5����DEC�Ƶ�C˳ʱ����ת��
����ͼ2������Dǡ������BC���ӳ�����ʱ����AP�ij���
������תһ�ܵĹ����У����PAB�����ΪS����S����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
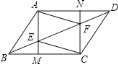
����Ŀ����ͼ��ƽ���ı���![]() �У���
����![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ������
������![]() ��
��![]() ��
��
![]() ��֤��
��֤��![]() ��
��
![]() ���ı���
���ı���![]() ����ʲô����ʱ���ı���
����ʲô����ʱ���ı���![]() �����Σ�֤����Ľ��ۣ�
�����Σ�֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Rt��ABC����ֱ�DZߵij��ֱ�Ϊ6cm��8cm�����������Բ�İ뾶������Բ�뾶�ı�Ϊ��_________����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ���ֱ�ֱ��
���ֱ�ֱ��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��
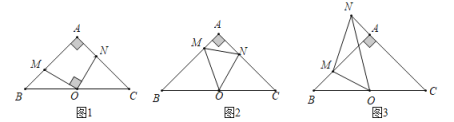
��1����ͼ1����![]() ʱ����֤��
ʱ����֤��![]() ��
��
��2����ͼ2����![]() ʱ���߶�
ʱ���߶�![]() ��
��![]() ��
��![]() ֮���к�������ϵ��֤����Ľ��ۣ�
֮���к�������ϵ��֤����Ľ��ۣ�
��3����ͼ3����![]() ʱ����ת
ʱ����ת![]() �����߶�֮��
�����߶�֮��![]() ��
��![]() ��
��![]() �к�������ϵ��֤����Ľ��ۣ�
�к�������ϵ��֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����10��10�������У�ÿ�����Ӷ��DZ߳�Ϊ1��С�����Σ���֪��ABC�������������ֱ�ΪA(1��1)��B(4��2)��C(3��4)��
(1)�뻭������ABC�Ƶ�A˳ʱ����ת90����õ��ġ�AB1C1��
(2)�뻭����ABC����ԭ��O�����ĶԳƵġ�A2B2C2��
(3)����ABC�Ƶ�A˳ʱ����ת90����õ���AB1C1�����C��������·������
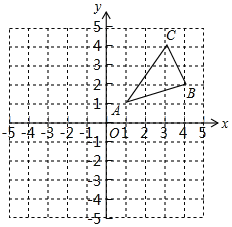
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
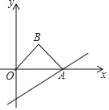
����Ŀ����ͼ��ֱ��y��![]() x��2��x�ύ�ڵ�A����OAΪб����x���Ϸ�������ֱ��������OAB������OAB��x������ƽ�ƣ�����B����ֱ��y��
x��2��x�ύ�ڵ�A����OAΪб����x���Ϸ�������ֱ��������OAB������OAB��x������ƽ�ƣ�����B����ֱ��y��![]() x��2��ʱ������OABƽ�Ƶľ�����_____��
x��2��ʱ������OABƽ�Ƶľ�����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
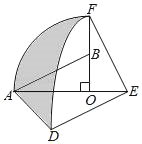
����Ŀ����ͼ����Rt��AOB�У���AOB=90�㣬OA=2��OB=1����Rt��AOB�Ƶ�O˳ʱ����ת90����õ�Rt��FOE�����߶�EF�Ƶ�E��ʱ����ת90����õ��߶�ED���քe��O��EΪԲ�ģ�OA��ED��Ϊ�뾶����AF�ͻ�DF������AD����ͼ����Ӱ���ֵ������__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ�λΪ1�ķ���ֽ�ϣ���A1A2A3����A3A4A5����A5A6A7����������б����x���ϣ�б�߳��ֱ�Ϊ2��4��6�����ĵ�ֱ�������Σ�����A1A2A3�Ķ�������ֱ�ΪA1��2��0����A2��1��1����A3��0��0��������ͼ����ʾ���ɣ�A2019������Ϊ�� ��
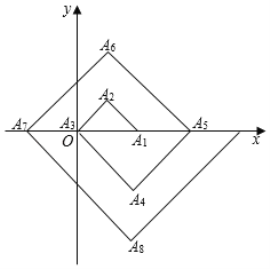
A.����1008��0��B.����1006��0��C.��2����504��D.��1��505��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com