
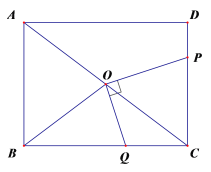
【题目】如图,在长方形ABCD中,AB=6,BC=8,点O在对角线AC上,且OA=OB=OC,点P是边CD上的一个动点,连接OP,过点O作OQ⊥OP,交BC于点Q.
(1)求OB的长度;
(2)设DP= x,CQ= y,求y与x的函数表达式(不要求写自变量的取值范围);
(3)若![]() OCQ是等腰三角形,求CQ的长度.
OCQ是等腰三角形,求CQ的长度.
【答案】(1)5;(2)![]() ;(3)当
;(3)当![]() 或
或![]() 时,⊿OCQ是等腰三角形.
时,⊿OCQ是等腰三角形.
【解析】
(1)利用勾股定理先求出AC的长,继而根据已知条件即可求得答案;
(2)延长QO交AD于点E,连接PE、PQ ,先证明△AEO≌△CQO,从而得OE=OQ,AE=CQ=y,由垂直平分线的性质可得PE=PQ,即![]() ,在Rt⊿EDP中,有
,在Rt⊿EDP中,有![]() ,在Rt⊿PCQ中,
,在Rt⊿PCQ中,![]() ,继而可求得答案;
,继而可求得答案;
(3)分CQ=CO,OQ=CQ,OQ=OC三种情况分别进行讨论即可求得答案.
(1)∵四边形ABCD是长方形,
∴∠ABC=90°,
∴![]() ,
,
∴OB=OA=OC=![]() ;
;
(2)延长QO交AD于点E,连接PE、PQ ,
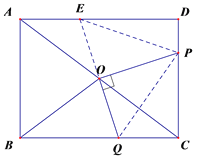
∵四边形ABCD是长方形,
∴CD=AB=6,AD=BC=8,AD//BC,
∴∠AEO=∠CQO,
在△COQ和△AOE中,
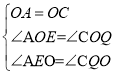 ,
,
∴△AEO≌△CQO(SAS),
∴OE=OQ,AE=CQ=y,
∴ED=AD-AE=8-y,
∵OP⊥OQ,
∴OP垂直平分EQ,
∴PE=PQ,
∴![]() ,
,
∵PD=x,
∴CP=CD-CP=6-x,
在Rt⊿EDP中,![]() ,
,
在Rt⊿PCQ中,![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)分三种情况考虑:
①如图,若CQ=CO时,此时CQ=CO=5;
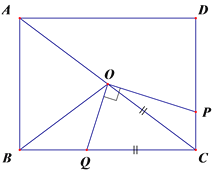
②如图,若OQ=CQ时,作OF⊥BC,垂足为点F,
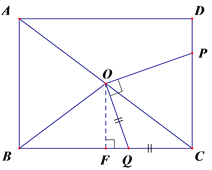
∵OB=OC,OF⊥BC,
∴BF=CF=![]() BC=4,
BC=4,
∴![]() ,
,
∵OQ=CQ,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
③若OQ=OC时,此时点Q与点B重合,点P在DC延长线上,此情况不成立,
综上所示,当![]() 或
或![]() 时,⊿OCQ是等腰三角形.
时,⊿OCQ是等腰三角形.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC内有一点D,且DA=DB=DC.若∠DAB=20°,∠DAC=30°,则∠BDC的度数为( )
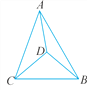
A. 100° B. 80° C. 70° D. 50°
查看答案和解析>>
科目:初中数学 来源: 题型:
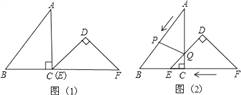
【题目】已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上,∠ACB=∠EDF=90°,∠DEF=45°,AC=8cm,BC=6cm,EF=9cm.如图(2),△DEF从图(1)的位置出发,以1cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2cm/s的速度沿BA匀速移动,当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动,DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5).
解答下列问题:
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式,是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由;
(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
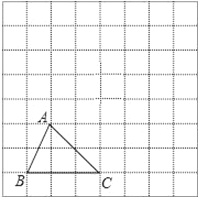
【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,![]() ABC的顶点均在格点上.
ABC的顶点均在格点上.
(1)先将![]() ABC向上平移4个单位后得到的
ABC向上平移4个单位后得到的![]() A1B1C1,再将
A1B1C1,再将![]() A1B1C1绕点C1按顺时针方向旋转90°后所得到的
A1B1C1绕点C1按顺时针方向旋转90°后所得到的![]() A2B2 C1,在图中画出
A2B2 C1,在图中画出![]() A1B1C1和
A1B1C1和![]() A2B2 C1.
A2B2 C1.
(2)![]() A2B2 C1能由
A2B2 C1能由![]() ABC绕着点O旋转得到,请在网格上标出点O.
ABC绕着点O旋转得到,请在网格上标出点O.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的面积为10cm2,它的两条对角线交于点O1,以AB、AO1为两邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2,同样以AB、AO2为两邻边作平行四边形ABC2O2,…,依此类推,则平行四边形ABCnOn的面积为( )

A. ![]() cm2B.
cm2B. ![]() cm2C.
cm2C. ![]() cm2D.
cm2D. ![]() cm2
cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,D为AB的中点,四边形BCED为平行四边形,DE,AC相交于F.连接DC,AE.
(1)试确定四边形ADCE的形状,并说明理由.
(2)若AB=16,AC=12,求四边形ADCE的面积.
(3)当△ABC满足什么条件时,四边形ADCE为正方形?请给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOD=160°,OB、OC、OM、ON是∠AOD内的射线.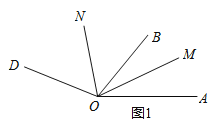
(1)如图1,若OM平分∠AOB,ON平分∠BOD.当OB绕点O在∠AOD内旋转时,求∠MON的大小;
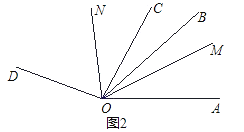
(2)如图2,若∠BOC=20°,OM平分∠AOC,ON平分∠BOD.当∠BOC绕点O在∠AOD内旋转时,求∠MON的大小;
(3)在(2)的条件下,若∠AOB=10°,当∠B0C在∠AOD内绕着点O以2度/秒的速度逆时针旋转t秒时,∠AOM=![]() ∠DON.求t的值.
∠DON.求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华将一条直角边长为1的一个等腰直角三角形纸片(如图1),沿它的对称轴折叠1次后得到一个等腰直角三角形(如图2),再将图2的等腰直角三角形沿它的对称轴折叠后得到一个等腰直角三角形(如图3),则图3中的等腰直角三角形的一条腰长为_________;同上操作,若小华连续将图1的等腰直角三角形折叠n次后所得到的等腰直角三角形(如图n+1)的一腰长为_________.
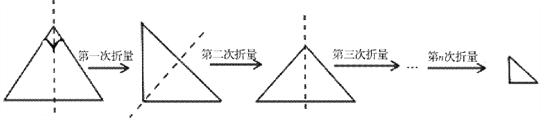
图1 图2 图3 图n+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com