
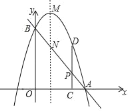
【题目】如图,已知直线y=﹣x+4分别交x轴、y轴于点A、B,抛物线过y=ax2+bx+c经过A,B两点,点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.
(1)若抛物线的解析式为y=﹣![]() x2+x+4,设其顶点为M,其对称轴交AB于点N.
x2+x+4,设其顶点为M,其对称轴交AB于点N.
①求点M、N的坐标;
②是否存在点P,使四边形MNPD为菱形?并说明理由;
(2)当点P的横坐标为2时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形是直角三角形?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.

【答案】(1)① M(1,![]() ),N(1,3); ②见解析;(2)见解析.
),N(1,3); ②见解析;(2)见解析.
【解析】
(1)①把二次函数表达式化为顶点式表达式,即可求解;
②不存在.理由如下:设点P 的坐标为(m,-m+4),则D(m,-![]() m2+m+4),PD=-
m2+m+4),PD=-![]() m2+m+4-(-m+4)=-
m2+m+4-(-m+4)=-![]() m2+2m,当四边形MNPD为平行四边形,则:
m2+2m,当四边形MNPD为平行四边形,则:![]() m2+2m=
m2+2m=![]() ,解得:m=1,则:点P(3,1),由N(1,3),则:PN=
,解得:m=1,则:点P(3,1),由N(1,3),则:PN=![]() ≠MN,即可求解;
≠MN,即可求解;
(2)分∠BDP=90°或∠PBD=90°两种情况,求解即可.
解:(1)①y=﹣![]() x2+x+4=﹣
x2+x+4=﹣![]() (x﹣1)2+
(x﹣1)2+![]() ,
,
∴顶点M的坐标为(1,![]() ),
),
当x=1时,y=﹣1+4=3,
∴点N的坐标为(1,3);
②不存在.理由如下:
MN=![]() ﹣3=
﹣3=![]() ,
,
设点P 的坐标为(m,﹣m+4),则D(m,﹣![]() m2+m+4),
m2+m+4),
PD=﹣![]() m2+m+4﹣(﹣m+4)=﹣
m2+m+4﹣(﹣m+4)=﹣![]() m2+2m,
m2+2m,
∵PD∥MN.
∴当PD=MN时,四边形MNPD为平行四边形,
即﹣![]() m2+2m=
m2+2m=![]() ,解得:m=1或3(m=1舍去),
,解得:m=1或3(m=1舍去),
∴点P(3,1),由N(1,3),
∴PN=![]() ≠MN,
≠MN,
∴平行四边形MNPD不是菱形,
即:不存在点P,使四边形MNPD为菱形;
(2)①当∠BDP=90°时,点P(2,2),则四边形BOCD为矩形,
∴D(2,4),又A(4,0),B(0,4),
∴抛物线的表达式为:y=﹣![]() x2+x+4;
x2+x+4;
②当∠PBD=90°时,△PBD为等腰直角三角形,
则PD=2xP=4,
∴D(2,6),又A(4,0),B(0,4),
把A、B、D坐标代入二次函数表达式得: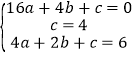 ,解得:
,解得: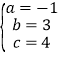 ,
,
故:二次函数表达式为:y=﹣x2+3x+4.


科目:初中数学 来源: 题型:
【题目】如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.

下面有三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;
②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.
其中合理的是( )
A. ① B. ② C. ①② D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
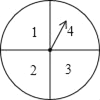
【题目】小王和小张利用如图所示的转盘做游戏,转盘的盘面被分为面积相等的4个扇形区域,且分别标有数字1,2,3,4.游戏规则如下:两人各转动转盘一次,分别记录指针停止时所对应的数字,如两次的数字都是奇数,则小王胜;如两次的数字都是偶数,则小张胜;如两次的数字是奇偶,则为平局.解答下列问题:
(1)小王转动转盘,当转盘指针停止,对应盘面数字为奇数的概率是多少?
(2)该游戏是否公平?请用列表或画树状图的方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠CAB=30°,将△ABC在平面内绕点A逆时针旋转到△AB'C'的位置,且CC'∥AB,则旋转角的度数为( )

A. 100° B. 120° C. 110° D. 130°
查看答案和解析>>
科目:初中数学 来源: 题型:
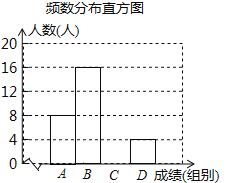
【题目】“品中华诗词,寻文化基因”.某校举办了第二届“中华诗词大赛”,将该校八年级参加竞赛的学生成绩统计后,绘制了如下不完整的频数分布统计表与频数分布直方图.
频数分布统计表
组别 | 成绩x(分) | 人数 | 百分比 |
A | 60≤x<70 | 8 | 20% |
B | 70≤x<80 | 16 | m% |
C | 80≤x<90 | a | 30% |
D | 90≤<x≤100 | 4 | 10% |
请观察图表,解答下列问题:
(1)表中a= ,m= ;
(2)补全频数分布直方图;
(3)D组的4名学生中,有1名男生和3名女生.现从中随机抽取2名学生参加市级竞赛,则抽取的2名学生恰好是一名男生和一名女生的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象与
的图象与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,
两点,![]() 是坐标原点.
是坐标原点.
(1)求交点![]() 、
、![]() 的坐标,并画出该一次函数的图象;
的坐标,并画出该一次函数的图象;
(2)求![]() 的面积;
的面积;
(3)根据图象直接写出:当![]() 时,
时,![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
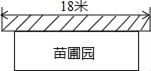
【题目】晨光中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米.
(1)若平行于墙的一边长为y米,直接写出y与x的函数关系式及其自变量x的取值范围;
(2)设这个苗圃园的面积为S,求S与x之间的函数关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车产业的发展,有效促进我国现代化建设.某汽车销售公司2015年盈利1500万元,到2017年盈利2160万元,且从2015年到2017年,每年盈利的年增长率相同.
(1)求平均年增长率?
(2)若该公司盈利的年增长率继续保持不变,预计2018年盈利多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com