
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,∠BAC=90°,AB=AC,D点在AC上,E点在BA的延长线上,BD=CE,BD的延长线交CE于F.证明:
如图,∠BAC=90°,AB=AC,D点在AC上,E点在BA的延长线上,BD=CE,BD的延长线交CE于F.证明:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某中学准备在校园里利用围墙一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,若设计一种砌法,使矩形花园的面积为300m2,则AB的长度为?
如图,某中学准备在校园里利用围墙一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,若设计一种砌法,使矩形花园的面积为300m2,则AB的长度为?查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
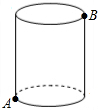 如图所示,有一圆柱,其高为8cm,它的底面直径为4cm,在圆柱的A处有一只蚂蚁,它想得到B处的食物,则蚂蚁经过的最短距离为10cm.(π取3)
如图所示,有一圆柱,其高为8cm,它的底面直径为4cm,在圆柱的A处有一只蚂蚁,它想得到B处的食物,则蚂蚁经过的最短距离为10cm.(π取3)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com