
分析 (1)①当0≤x≤3000时,按每吨收费1.8元收费;②当x>3000吨时,前面3000吨按每吨收费1.8元,其余(x-3000)吨按每吨收费2元收费;
(2)当x=3200时,按②付费,所以把x=3200代入②中的解析式中计算即可;
(3)由于9400>1.8×3000,则按②付费,所以2x-600=9400,然后解一元一次方程即可.
解答 解:(1)①当0≤x≤3000时,y=1.8x;
②当x>3000吨时,y=1.8×3000+2(x-30000)=2x-600;
(2)当x=3200时,y=2x-600=2×3200-600=5800(元);
(3)∵y=9400>1.8×3000,
∴该公司这月用水超过3000吨,
∴2x-600=9400x=5000.
答:这月该公司用水5000吨.故答案为y=1.8x,y=2x-600;5800.
点评 本题考查了一次函数的应用:分段函数是在不同区间有不同对应方式的函数,要特别注意自变量取值范围的划分,既要科学合理,又要符合实际.解决本题的关键是弄清楚每月用水量x(吨)与每吨收费的关系.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
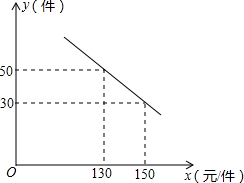 网购的普及标志着我国零售业进入了电商时代.某淘宝网店购进一种成本为100元/件的新商品,在试销中发现:销售单价x(元)与每天销售量y(件)之间满足如图所示的关系.
网购的普及标志着我国零售业进入了电商时代.某淘宝网店购进一种成本为100元/件的新商品,在试销中发现:销售单价x(元)与每天销售量y(件)之间满足如图所示的关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,直线AB,CD相交于点O,已知∠AOC=80°,OE把∠BOD分成两部分,且∠BOE:∠EOD=2:3,求∠EOD和∠AOE的度数.
如图所示,直线AB,CD相交于点O,已知∠AOC=80°,OE把∠BOD分成两部分,且∠BOE:∠EOD=2:3,求∠EOD和∠AOE的度数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com