
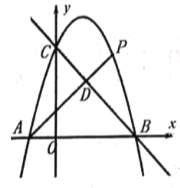
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 的抛物线
的抛物线![]() 与
与![]() 轴的另一个交点为
轴的另一个交点为![]() .
.
(1)求抛物线的解析式和点![]() 的坐标;
的坐标;
(2)![]() 是直线
是直线![]() 上方抛物线上一动点,
上方抛物线上一动点,![]() 交
交![]() 于
于![]() .设
.设![]() ,请求出
,请求出![]() 的最大值和此时点
的最大值和此时点![]() 的坐标;
的坐标;
(3)![]() 是
是![]() 轴上一动点,连接
轴上一动点,连接![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得线段
得线段![]() ,若点
,若点![]() 恰好落在抛物线上,请直接写出此时点
恰好落在抛物线上,请直接写出此时点![]() 的坐标.
的坐标.
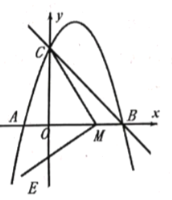
备用图
【答案】(1)![]() ,点
,点![]() 的坐标为
的坐标为![]() ;(2)
;(2)![]() 的最大值为
的最大值为![]() ,此时
,此时![]() ;(3)(
;(3)(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
【解析】
(1)把点B(3,0)代入![]() 先求得c的值,再求得点C的坐标,利用待定系数法即可求得抛物线的解析式和点A的坐标;
先求得c的值,再求得点C的坐标,利用待定系数法即可求得抛物线的解析式和点A的坐标;
(2)设点P的横坐标为![]() ,作
,作![]() 轴于N,交BC于M,先用m表示出
轴于N,交BC于M,先用m表示出![]() ,再作
,再作![]() 于E,
于E,![]() 于F,得到
于F,得到![]() ,即
,即![]() ,推出
,推出![]() ,得到
,得到 ,利用二次函数的性质即可求解;
,利用二次函数的性质即可求解;
(3)过M,E分别作![]() 轴,
轴,![]() 轴的垂线交于H,设点M的坐标为(
轴的垂线交于H,设点M的坐标为(![]() ,
,![]() ),证得
),证得![]() ,得到点E的坐标为(
,得到点E的坐标为(![]() ,
,![]() ),代入
),代入![]() 即可得n的值,即可求解.
即可得n的值,即可求解.
(1)∵![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点C,
轴交于点C,
∴![]() ,解得
,解得![]() ,
,
∴![]() ,
,
∵抛物线![]() 经过点B,C,
经过点B,C,
∴![]()
解得![]() ,
,
∴抛物线解析式为![]() ;
;
当![]() 时,
时,![]() ,
,
解得:![]()
∴点![]() 的坐标为
的坐标为![]() ;
;
(2)设点P的横坐标为![]() ,连接PC,PB,过P作
,连接PC,PB,过P作![]() 轴于N,交BC于M,
轴于N,交BC于M,
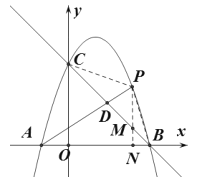
由(1)知:直线![]() 的解析式为
的解析式为![]() ,
,
∴![]() ,
,
则![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
![]()
![]()
![]() ,
,
连接AC,分别过A,P作![]() 于E,
于E,![]() 于F,
于F,
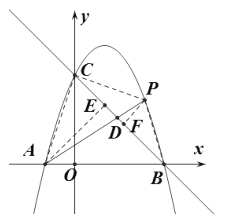
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]()
∴![]() ,
,
∵![]() ,
,
∴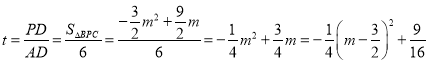 ,
,
∴当![]() 时,
时,![]() 的最大值为
的最大值为![]() ,此时
,此时![]() ;
;
(3)过M,E分别作![]() 轴,
轴,![]() 轴的垂线交于H,
轴的垂线交于H,
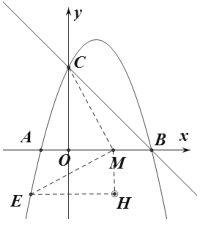
∴∠H=90![]() ,∠MEH=∠OME,
,∠MEH=∠OME,
根据旋转的性质知:∠CME=90![]() ,EM=MC,
,EM=MC,
∴∠CMO+∠OME=90![]() ,∠CMO+∠MCO=90
,∠CMO+∠MCO=90![]() ,
,
∴∠MEH=∠MCO,
设点M的坐标为(![]() ,
,![]() ),
),
根据题意将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得线段
得线段![]() ,若点
,若点![]() 恰好落在抛物线上,
恰好落在抛物线上,
则点M在![]() 轴正半轴上,即
轴正半轴上,即![]() ,
,
在Rt△MEH和Rt△MCO中,
 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴点E的坐标为:(![]() ,
,![]() ),
),
把代入E (![]() ,
,![]() ) 代入
) 代入![]() ,
,
整理得:![]() ,
,
解得![]() ,
,![]() .
.
∴点M的坐标为:(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
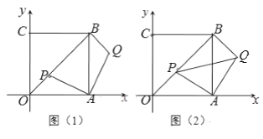
【题目】平面直角坐标系中,四边形OABC是正方形,点A,C 在坐标轴上,点B(![]() ,
,![]() ),P是射线OB上一点,将
),P是射线OB上一点,将![]() 绕点A顺时针旋转90°,得
绕点A顺时针旋转90°,得![]() ,Q是点P旋转后的对应点.
,Q是点P旋转后的对应点.
(1)如图(1)当OP = ![]() 时,求点Q的坐标;
时,求点Q的坐标;
(2)如图(2),设点P(![]() ,
,![]() )(
)(![]() ),
),![]() 的面积为S. 求S与
的面积为S. 求S与![]() 的函数关系式,并写出当S取最小值时,点P的坐标;
的函数关系式,并写出当S取最小值时,点P的坐标;
(3)当BP+BQ = ![]() 时,求点Q的坐标(直接写出结果即可)
时,求点Q的坐标(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好地做好复课准备,某班家委会讨论决定购买![]() 两种型号的口罩供班级学生使用,已知
两种型号的口罩供班级学生使用,已知![]() 型口罩每包价格
型口罩每包价格![]() 元,
元,![]() 型口罩每包价格比
型口罩每包价格比![]() 型少4元,180元钱购买的
型少4元,180元钱购买的![]() 型口罩比
型口罩比![]() 型口罩少12包.
型口罩少12包.
(1)求![]() 的值;
的值;
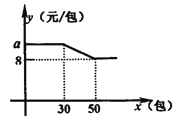
(2)经与商家协商,购买![]() 型口罩价格可以优惠,其中每包价格
型口罩价格可以优惠,其中每包价格![]() (元)和购买数量
(元)和购买数量![]() (包)的函数关系如图所示,
(包)的函数关系如图所示,![]() 型口罩一律按原价销售.
型口罩一律按原价销售.
①求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
②若家委会计划购买![]() 型、
型、![]() 型共计100包,其中
型共计100包,其中![]() 型不少于30包,且不超过60包.问购买
型不少于30包,且不超过60包.问购买![]() 型口罩多少包时,购买口罩的总金额最少,最少为多少元?
型口罩多少包时,购买口罩的总金额最少,最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
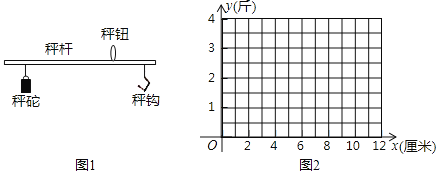
【题目】我国传统的计重工具﹣﹣秤的应用,方便了人们的生活.如图1,可以用秤砣到秤纽的水平距离,来得出秤钩上所挂物体的重量.称重时,若秤杆上秤砣到秤纽的水平距离为x(厘米)时,秤钩所挂物重为y(斤),则y是x的一次函数.下表中为若干次称重时所记录的一些数据.
x(厘米) | 1 | 2 | 4 | 7 | 11 | 12 |
y(斤) | 0.75 | 1.00 | 1.50 | 2.75 | 3.25 | 3.50 |
(1)在上表x,y的数据中,发现有一对数据记录错误.在图2中,通过描点的方法,观察判断哪一对是错误的?
(2)根据(1)的发现,问秤杆上秤砣到秤纽的水平距离为16厘米时,秤钩所挂物重是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织了一次创建全国文明城市知识竞赛活动,有30名同学参加这次竞赛,成绩分布频数表如下:(单位:分)
成绩(分) | 组中值 | 频数(人数) |
80.5~85.5 | 83 | 3 |
85.5~90.5 | 88 | 6 |
90.5~95.5 | 93 | 12 |
95.5~100.5 | 98 | 9 |
(1)利用组中值计算这30位同学的平均数;
(2)学校根据这次竞赛成绩从高到低选15位同学参加市级比赛,小明同学也参加了这次竞赛,知道自己的成绩后,他想知道自己是否有资格参加市里比赛(学校还未公布到市里比赛名单),他最应关注频数,平均分,众数,中位数中的哪个量?请说明理由;
(3)“创文知识竞赛”中,获一等奖的小红同学得到了印有龚扇、剪纸、彩灯图案的三枚纪念章,她从中选取两枚送给弟弟,则小红送给弟弟的两枚纪念章中,恰好有彩灯图案的概率是多少?请用树状图或列表法说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3700米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B处,此时观测目标C的俯角是50°.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20)
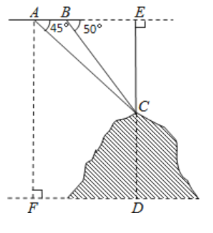
(1)直接写出∠ACB的大小;
(2)求这座山的高度CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
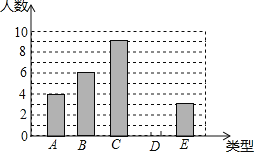
【题目】某单位750名职工积极参加向贫困地区学校捐书活动,为了解职工的捐数量,采用随机抽样的方法抽取30名职工作为样本,对他们的捐书量进行统计,统计结果共有4本、5本、6本、7本、8本五类,分别用A、B、C、D、E表示,根据统计数据绘制成了如图所示的不完整的条形统计图,由图中给出的信息解答下列问题:
(1)补全条形统计图;
(2)求这30名职工捐书本数的平均数、众数和中位数;
(3)估计该单位750名职工共捐书多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
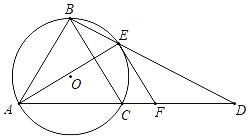
【题目】如图,⊙O是△ABC的外接圆,AB=BC,延长AC到点D,使得CD=CB,连接BD交⊙O于点E,过点E做BC的平行线交CD于点F.
(1)求证:AE=DE.
(2)求证:EF为⊙O的切线;
(3)若AB=5,BE=3,求弦AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com