
【题目】在平面直角坐标系中,二次函数y=﹣x2+6x﹣9的图象顶点为A,与y轴交于点B.若在该二次函数图形上取一点C,在x轴上取一点D,使得四边形ABCD为平行四边形,则D点的坐标为( )
A.(﹣9,0)
B.(﹣6,0)
C.(6,0)
D.(9,0)
【答案】D
【解析】如图:
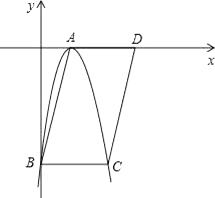
∵y=﹣x2+6x﹣9=﹣(x﹣3)2,
∴顶点A的坐标为(3,0),
令x=0得到y=﹣9,
∴点B的坐标为(0,﹣9),
令y=﹣x2+6x﹣9=﹣9,解得:x=0或x=6,
∴点C的坐标为(6,﹣9),
∴BC=AD=6,
∴OD=OA+AD=3+6=9,
∴点D的坐标为(9,0),
所以答案是:D.
【考点精析】认真审题,首先需要了解二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小),还要掌握二次函数的最值(如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a)的相关知识才是答题的关键.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,D为BC边上的一点,延长AD到点E,连接BE、CE,
∠ABD+![]() ∠3=90°,∠1=∠2=∠3,下列结论:①△ABD为等腰三角形;②AE=AC;③BE=CE=CD;④CB平分∠ACE.其中正确的结论个数有( )
∠3=90°,∠1=∠2=∠3,下列结论:①△ABD为等腰三角形;②AE=AC;③BE=CE=CD;④CB平分∠ACE.其中正确的结论个数有( )
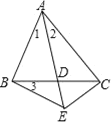
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,AD=6,将矩形ABCD绕点B按顺时针方向旋转后得到矩形A′BC′D′.若边A′B交线段CD于H,且BH=DH,则DH的值是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在△ ABC中,AD,AE分别是 △ ABC的高和角平分线,若∠B=30°,∠C=50°.
(1)求∠DAE的度数.
(2)试写出 ∠DAE与∠C-∠B有何关系?(不必证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
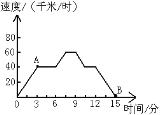
【题目】观察下图,回答问题.
(1)反映了哪两个变量之间的关系?
(2)点A,B分别表示什么?
(3)说一说速度是怎样随时间变化而变化的;
(4)你能找到一个实际情境,大致符合下图所刻画的关系吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一张等腰直角三角形彩色纸,将斜边上的高线四等分,然后裁出三张宽度相等的长方形纸条,若恰好可以用这些纸条为一幅正方形美术作品镶边(纸条不重叠),则这张彩色纸的面积与镶嵌所得的作品(如图2)面积之比为( )
A.2:3
B.3:4
C.1:1
D.4:3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个长为8分米,宽为5分米,高为7分米的长方体上,截去一个长为6分米,宽为5分米,深为2分米的长方体后,得到一个如图所示的几何体.一只蚂蚁要从该几何体的顶点A处,沿着几何体的表面到几何体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是 分米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,0为原点,A(4,0),E(0,3),四边形OABC,四边形OCDE都为平行四边形,OC=5,函数y= ![]() (x>0)的图象经过AB的中点F和DE的中点G,则k的值为 .
(x>0)的图象经过AB的中点F和DE的中点G,则k的值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°,点D在边OA上,将图中的△COD绕点O按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,在第________秒时,边CD恰好与边AB平行.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com