
【题目】在矩形ABCD中,![]() ,点G,H分别在边AB,DC上,且HA=HG,点E为AB边上的一个动点,连接HE,把△AHE沿直线HE翻折得到△FHE.
,点G,H分别在边AB,DC上,且HA=HG,点E为AB边上的一个动点,连接HE,把△AHE沿直线HE翻折得到△FHE.
(1)如图1,当DH=DA时,
①填空:∠HGA= 度;
②若EF∥HG,求∠AHE的度数,并求此时a的最小值;
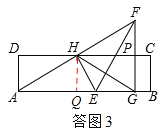
(2)如图3,∠AEH=60°,EG=2BG,连接FG,交边FG,交边DC于点P,且FG⊥AB,G为垂足,求a的值.

【答案】(1)①45;②当∠AHE为锐角时,∠AHE=22.5°时,a的最小值是2;当∠AHE为钝角时,∠AHE=112.5°时,a的最小值是![]() ;(2)
;(2)![]() .
.
【解析】
(1)①∵四边形ABCD是矩形,∴∠ADH=90°.
∵DH=DA,∴∠DAH=∠DHA=45°.∴∠HAE=45°.
∵HA=HG,∴∠HAE=∠HGA=45°
②分两种情况讨论:
第一种情况:如答图1,∠AHE为锐角时,
∵∠HAG=∠HGA=45°,∴∠AHG=90°.
由折叠可知:∠HAE=∠F=45°,∠AHE=∠FHE,
∵EF∥HG,∴∠FHG=∠F=45°.
∴∠AHF=∠AHG![]() ∠FHG=45°,即∠AHE+∠FHE=45°.
∠FHG=45°,即∠AHE+∠FHE=45°.
∴∠AHE=22.5°.
此时,当B与G重合时,a的值最小,最小值是2.

第二种情况:如答图2,∠AHE为钝角时,
∵EF∥HG,∴∠HGA=∠FEA=45°,即∠AEH+∠FEH=45°.
由折叠可知:∠AEH=∠FEH,∴∠AEH=∠FEH=22.5°.
∵EF∥HG,∴∠GHE=∠FEH=22.5°.
∴∠AHE=90°+22.5°=112.5°.
此时,当B与E重合时,a的值最小,
设DH=DA=x,则AH=CH=![]() x,
x,
在Rt△AHG中,∠AHG=90°,由勾股定理得:AG=![]() AH=2x,
AH=2x,
∵∠AEH=∠FEH,∠GHE=∠FEH,∴∠AEH=∠GHE.∴GH=GE=![]() x.
x.
∴AB=AE=2x+![]() x.
x.
∴a的最小值是![]() .
.
综上所述,当∠AHE为锐角时,∠AHE=22.5°时,a的最小值是2;当∠AHE为钝角时,∠AHE=112.5°时,a的最小值是![]() .
.

(2)如答图3:过点H作HQ⊥AB于Q,则∠AQH=∠GQH=90°,
在矩形ABCD中,∠D=∠DAQ=90°,
∴∠D=∠DAQ=∠AQH=90°.
∴四边形DAQH为矩形.∴AD=HQ.
设AD=x,GB=y,则HQ=x,EG=2y,
由折叠可知:∠AEH=∠FEH=60°,∴∠FEG=60°.
在Rt△EFG中,EG=EF×cos60°=2y,
在Rt△HQE中,![]() ,
,
∴![]() .
.
∵HA=HG,HQ⊥AB,∴AQ=GQ=![]() .
.
∴AE=AQ+QE=![]() .
.
由折叠可知:AE=EF,即![]() ,即
,即![]() .
.
∴AB=2AQ+GB= .
.
∴ .
.


科目:初中数学 来源: 题型:
【题目】2019年4月23日是第24个世界读书日.为了弘扬中华传统文化,我县某学校举办了“让读书成为习惯,让书香飘满校园”主题活动,为此特为每个班级订购了一批新的图书.初一(1)班订购老舍文集4套和四大名著2套,总费用为480元;初一(2)班订购老舍文集2套和四大名著3套,总费用为520元.
(1)求老舍文集和四大名著每套各是多少元?
(2)学校准备再购买老舍文集和四大名著共20套,总费用不超过1720元,购买老舍文集的数量不超过四大名著的3倍,问学校有几种购买方案,请你设计出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,是用3根相同火柴棒拼成的一个三角图形,记为一个基本图形,将此基本图形不断的复制,使得相邻的两个基本图形的边重合,这样得到图②,图③…
(1)观察以上图形,图④中所用火柴棒的根数为_________,
猜想:在图n中,所用火柴棒的根数为_________(用n表示);
(2)如图,将图n放在直角坐标系中,设其中第一个基本图形的中心O1的坐标为(![]() ,
,![]() ),则
),则![]() =_________;
=_________;![]() 的坐标为_________.
的坐标为_________.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“安全教育,警钟长鸣”,某校随机抽取了部分学生就安全知识的了解情况进行问卷调查,其中“很好”“较好”“一般”“较差”四类学生分别占调查学生数的25%,50%,20%,5%.
(1)选择合适的统计图描述上面的数据;
(2)根据上面的调查结果,若该校有1400名学生,则对安全知识了解“较差”的学生有多少名?
(3)根据以上信息,请提出一条合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是⊙
是⊙![]() 的直径,弦
的直径,弦![]() 与
与![]() 交于点
交于点![]() ,过点
,过点![]() 作⊙
作⊙![]() 的切线与
的切线与![]() 的延长线交于点
的延长线交于点![]() ,
, ![]() 交直线
交直线![]() 于点
于点![]() .
.
(![]() )若
)若![]() ,求证:
,求证: ![]() 是⊙
是⊙![]() 的切线;
的切线;
(![]() )如果
)如果![]() ,
, ![]() 且
且![]() 为
为![]() 的中点,求直径
的中点,求直径![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列一段文字,再解答问题:
已知在平面内有两点![]() ,
,![]() ,其两点间的距离公式为
,其两点间的距离公式为![]() ;同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为
;同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为![]() 或
或![]() .
.
(1)已知点A(2,4),B(-2,1),则AB=__________;
(2)已知点C,D在平行于y轴的直线上,点C的纵坐标为4,点D的纵坐标为-2,则CD=__________;
(3)已知点P(3,1)和(1)中的点A,B,判断线段PA,PB,AB中哪两条线段的长是相等的?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
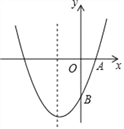
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且经A(1,0)、
B(0,﹣3)两点.(1)求抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上,是否存在点M,使它到点A的距离与到点B的距离之和最小,如果存在求出点M的坐标,如果不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com