
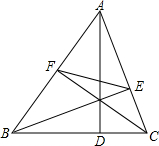
 如图,△ABC的三条高为AD、BE、CF,且AB=6,BC=5,EF=3,则sin∠BAC的值为( )
如图,△ABC的三条高为AD、BE、CF,且AB=6,BC=5,EF=3,则sin∠BAC的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
| AE |
| AB |
| EF |
| BC |
 解:如图,∵BE⊥AC,CF⊥AB,
解:如图,∵BE⊥AC,CF⊥AB,| AE |
| AB |
| EF |
| BC |
| BE |
| AB |
| 4 |
| 5 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 已知:△ABC是等边三角形.
已知:△ABC是等边三角形.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图是某校举行数学活动节的会徽轮廓图案在直角坐标系中的大致位置,它由相同对称轴的两条抛物线组成,有下列判断:①h>0;②m>0;③a>b;④m>n,其中正确的个数有( )
如图是某校举行数学活动节的会徽轮廓图案在直角坐标系中的大致位置,它由相同对称轴的两条抛物线组成,有下列判断:①h>0;②m>0;③a>b;④m>n,其中正确的个数有( )| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
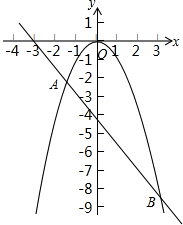 如图所示,抛物线y1=-x2与直线y2=-
如图所示,抛物线y1=-x2与直线y2=-| 3 |
| 2 |
| 9 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
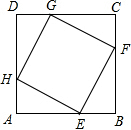 如图,在正方形ABCD中,E,F,G,H分别是边AB,BC,CD,DA上的点,且AE=BF=CG=DH,试判定四边形EFGH的形状,并证明你的结论.
如图,在正方形ABCD中,E,F,G,H分别是边AB,BC,CD,DA上的点,且AE=BF=CG=DH,试判定四边形EFGH的形状,并证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:
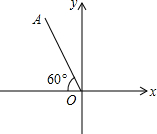 如图,OA=2,OA与x轴负半轴的夹角是60°,点A关于y轴的对称点是点A′,点P是x轴上一动点,当PA+PA′的值最小时,点P的坐标是( )
如图,OA=2,OA与x轴负半轴的夹角是60°,点A关于y轴的对称点是点A′,点P是x轴上一动点,当PA+PA′的值最小时,点P的坐标是( )| A、(-1,0) | ||
| B、(1,0) | ||
| C、(0,0) | ||
D、(
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com