
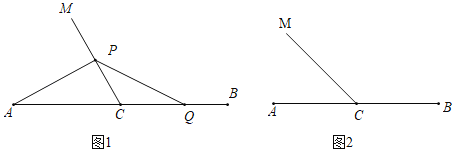
【题目】已知C为线段AB中点,∠ACM=α.Q为线段BC上一动点(不与点B重合),点P在射线CM上,连接PA,PQ,记BQ=kCP.
(1)若α=60°,k=1,
①如图1,当Q为BC中点时,求∠PAC的度数;
②直接写出PA、PQ的数量关系;
(2)如图2,当α=45°时.探究是否存在常数k,使得②中的结论仍成立?若存在,写出k的值并证明;若不存在,请说明理由.
【答案】(1)①详见解析;②PA=PQ.(2)存在![]() ,使得②中的结论成立.
,使得②中的结论成立.
【解析】
(1)①如图1,作辅助线,构建等边三角形,证明△ADC为等边三角形.根据等边三角形三线合一可得∠PAC=∠PAD=30°;
②根据①中得结论:∠PAC=∠PQC=30°,则PA=PQ;
(2)存在k=![]() ,如图2,作辅助线,构建全等三角形,证明△PAD≌△PQC(SAS).可得结论.
,如图2,作辅助线,构建全等三角形,证明△PAD≌△PQC(SAS).可得结论.
解:(1)①如图1,在CM上取点D,使得CD=CA,连接AD,

∵∠ACM=60°,
∴△ADC为等边三角形.
∴∠DAC=60°.
∵C为AB的中点,Q为BC的中点,
∴AC=BC=2BQ.
∵BQ=CP,
∴AC=BC=CD=2CP.
∴AP平分∠DAC.
∴∠PAC=∠PAD=30°.
②∵△ADC是等边三角形,
∴∠ACP=60°,
∵PC=CQ,
∴∠PQC=∠CPQ=30°,
∴∠PAC=∠PQC=30°,
∴PA=PQ;
(2)存在![]() ,使得②中的结论成立.
,使得②中的结论成立.
证明:过点P作PC的垂线交AC于点D.
∵∠ACM=45°,
∴∠PDC=∠PCD=45°.
∴PC=PD,∠PDA=∠PCQ=135°.
∵![]() ,,
,,![]()
∴CD=BQ.
∵AC=BC,
∴AD=CQ.
∴△PAD≌△PQC(SAS).
∴PA=PQ.


科目:初中数学 来源: 题型:
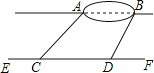
【题目】小明想测量湿地公园内某池塘两端A,B两点间的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=40°,再向前行走100米到点D处,测得∠BDF=52.44°,若直线AB与EF之间的距离为60米,求A,B两点的距离(结果精确到0.1)(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin52.44°≈0.79,cos52.44°≈0.61,tan52.44°≈1.30)
查看答案和解析>>
科目:初中数学 来源: 题型:
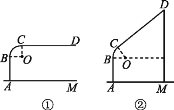
【题目】如图是一个桌面会议话筒示意图,中间BC部分是一段可弯曲的软管,在弯曲时可形成一段圆弧,设圆弧所在圆的圆心为O,线段AB,CD均与圆弧相切,点B,C分别为切点,已知AB的长10 cm,CD的长为25.2 cm.
(1)如图①,若话筒弯曲后CD与桌面AM平行,此时CD距离桌面14 cm,求弧BC的长度(结果保留π);
(2)如图②,若话筒弯曲后弧BC所对的圆心角度数为60°,求话筒顶端D到桌面AM的距离(结果保留一位小数).(参考数据:![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,有一个可以自由转动的转盘,其盘面分为4等份,在每一等份分别标有对应的数字2,3,4,5.小明打算自由转动转盘10次,现已经转动了8次,每一次停止后,小明将指针所指数字记录如下:
次数 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 | 第8次 | 第9次 | 第10次 |
数字 | 3 | 5 | 2 | 3 | 3 | 4 | 3 | 5 |
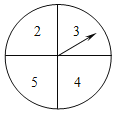
(1)求前8次的指针所指数字的平均数.
(2)小明继续自由转动转盘2次,判断是否可能发生“这10次的指针所指数字的平均数不小于3.3,且不大于3.5”的结果?若有可能,计算发生此结果的概率,并写出计算过程;若不可能,说明理由.(指针指向盘面等分线时为无效转次.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市随机选取1000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.假定每位顾客购买商品的可能性相同.
商品 顾客人数 | 甲 | 乙 | 丙 | 丁 |
100 | √ | × | √ | √ |
217 | × | √ | × | √ |
200 | √ | √ | √ | × |
300 | √ | × | √ | × |
85 | √ | × | × | × |
98 | × | √ | × | × |
(1)估计顾客同时购买乙和丙的概率为__________.
(2)如果顾客购买了甲,并且同时也在乙、丙、丁中进行了选购,则购买__________(填乙、丙、丁)商品的可能性最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(3,m),B(﹣2,﹣3)是直线AB和某反比例函数的图象的两个交点.
(1)求直线AB和反比例函数的解析式;
(2)观察图象,直接写出当x满足什么范围时,直线AB在双曲线的下方;
(3)反比例函数的图象上是否存在点C,使得△OBC的面积等于△OAB的面积?如果不存在,说明理由;如果存在,求出满足条件的所有点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受地震的影响,某超市鸡蛋供应紧张,需每天从外地调运鸡蛋1200斤.超市决定从甲、乙两大型养殖场调运鸡蛋,已知甲养殖场每天最多可调出800斤,乙养殖场每天最多可调出900斤,从两养殖场调运鸡蛋到超市的路程和运费如表:
到超市的路程(千米) | 运费(元/斤千米) | |
甲养殖场 | 200 | 0.012 |
乙养殖场 | 140 | 0.015 |
(1)若某天调运鸡蛋的总运费为2670元,则从甲、乙两养殖场各调运了多少斤鸡蛋?
(2)设从甲养殖场调运鸡蛋x斤,总运费为W元,试写出W与x的函数关系式,怎样安排调运方案才能使每天的总运费最省?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图要求: I、过直线外一点作这条直线的垂线: II、 作线段的垂直平分线;III、过直线上一点作这条直线的垂线: IV、 作角的平分线.如图是按上述要求排乱顺序的尺规作图:
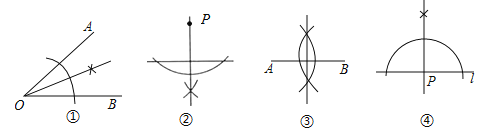
则正确的配对是( )
A.①-IV,②-II,③-I,④-IIIB.①-IV, ②-I,③-II,④-I
C.①-II,②-IV,③-1II,④-ID.①-IV,②-I,③-II,④-III
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com