
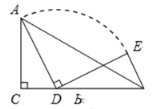
【题目】如图,在△ABC中,∠ACB 90,AC3,CB5,点D是CB边上的一个动点,将线段AD绕着点D 顺时针旋转90,得到线段DE,连结BE,则线段BE的最小值等于__________.
【答案】![]()
【解析】
根据题意过E作EF⊥BC于F,根据余角的性质得到∠DEF=∠ADC,根据全等三角形的性质得到DF=AC=3,EF=CD,设CD=x,根据勾股定理得到BE2=x2+(2-x)2=2(x-1)2+2,即可得到结论.
解:过E作EF⊥BC于F,
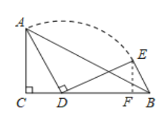
∵∠C=∠ADE=90°,
∴∠EFD=∠C=90°,∠FED+∠EDF=90°,∠EDF+∠ADC=90°,
∴∠DEF=∠ADC,
在△EDF和△DAC中,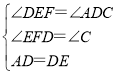 ,
,
∴△EDF≌△DAC(AAS),
∴DF=AC=3,EF=CD,
设CD=x,则BE2=x2+(2-x)2=2(x-1)2+2,
∴BE2的最小值是2,
∴BE的最小值是![]() .
.
故答案为:![]() .
.


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
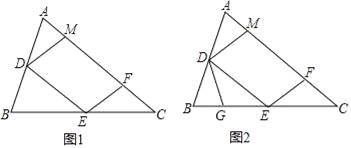
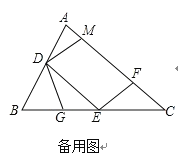
【题目】如图1,在锐角△ABC中,D、E分别是AB、BC的中点,点F在AC上,且满足∠AFE=∠A,DM∥EF交AC于点M.
(1)证明:DM=DA;
(2)如图2,点G在BE上,且∠BDG=∠C,求证:△DEG∽△ECF;
(3)在图2中,取CE上一点H,使得∠CFH=∠B,若BG=3,求EH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲车从A地到B地,乙车从B地到A地,乙车先出发先到达,甲乙两车之间的距离y(千米)与行驶的时间x(小时)的函数关系如图所示,则下列说法中不正确的是( )
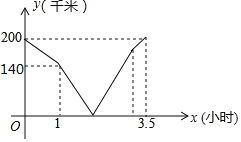
A.甲车的速度是80km/hB.乙车的速度是60km/h
C.甲车出发1h与乙车相遇D.乙车到达目的地时甲车离 B地10km
查看答案和解析>>
科目:初中数学 来源: 题型:
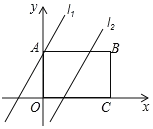
【题目】如图,在矩形ABCD中,点O为坐标原点,点B的坐标为(4,3),点A、C在坐标轴上,点P在BC边上,直线11:y=2x+3,直线12:y=2x﹣3.
(1)分别求直线11与x轴、直线12与AB的交点D和E的坐标;
(2)已知点M在矩形ABCD内部,且是直线12上的点,若△APM是等腰直角三角形,求点M的坐标;
(3)我们把直线11和直线12上的点所组成的图形称为图形F.已知矩形ANPQ的顶点N在图形F上,且在AP的上方,Q是坐标平面内的点,设N点的横坐标为x,请直接写出x的取值范围(不必说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
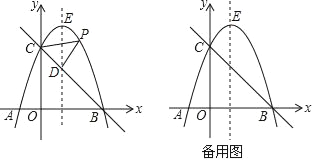
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交A(﹣1,0),B两点,与y轴交于点C(0,3),抛物线的顶点为点E.
(1)求抛物线的解析式;
(2)经过B,C两点的直线交抛物线的对称轴于点D,点P为直线BC上方抛物线上的一个动点,当点P运动到点E时,求△PCD的面积;
(3)点N在抛物线对称轴上,点M在x轴上,是否存在这样的点M与点N,使以M,N,C,B为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标(不写求解过程);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴,y轴分别交于点A,点B,抛物线
与x轴,y轴分别交于点A,点B,抛物线![]() 经过A,B与点
经过A,B与点![]() .
.
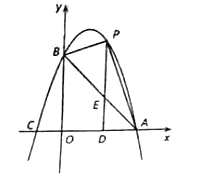
(1)求抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A,B重合),过点P作x轴的垂线,垂足为D,交线段AB于点E.设点P的横坐标为m.
①求![]() 的面积y关于m的函数关系式,当m为何值时,y有最大值,最大值是多少?
的面积y关于m的函数关系式,当m为何值时,y有最大值,最大值是多少?
②若点E是垂线段PD的三等分点,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王是“新星厂”的一名工人,请你阅读下列信息:
信息一:工人工作时间:每天上午8:00—12:00,下午14:00—18:00,每月工作25天;
信息二:小王生产甲、乙两种产品的件数与所用时间的关系见下表:
生产甲种产品数(件) | 生产乙种产品数(件) | 所用时间(分钟) |
10 | 10 | 350 |
30 | 20 | 850 |
信息三:按件计酬,每生产一件甲种产品得1.50元,每生产一件乙种产品得2.80元;
信息四:该厂工人每月收入由底薪和计酬工资两部分构成,小王每月的底薪为1900元.请根据以上信息,解答下列问题:
(1)小王每生产一件甲种产品和一件乙种产品分别需要多少分钟;
(2)2018年1月工厂要求小王生产甲种产品的件数不少于60件,则小王该月收入最多是多少元?此时小王生产的甲、乙两种产品分别是多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:四边形ABCD中,![]() ,
,![]() ,AD=CD,对角线AC,BD相交于点O,且BD平分∠ABC,过点A作
,AD=CD,对角线AC,BD相交于点O,且BD平分∠ABC,过点A作![]() ,垂足为H.
,垂足为H.
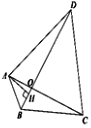
(1)求证:![]() ;
;
(2)判断线段BH,DH,BC之间的数量关系;并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市特产大闸蟹,2016年的销售额是![]() 亿元,因生态优质美誉度高,销售额逐年增加2018年的销售额达
亿元,因生态优质美誉度高,销售额逐年增加2018年的销售额达![]() 亿元,若2017、2018年每年销售额增加的百分率都相同.
亿元,若2017、2018年每年销售额增加的百分率都相同.
(1)求平均每年销售额增加的百分率;
(2)该市这![]() 年大闸蟹的总销售额是多少亿元?
年大闸蟹的总销售额是多少亿元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com