
分析 设直角三角形的两锐角分别为α,β,根据根与系数的关系表示出两根之和与两根之积,利用同角三角函数间的基本关系变形,再利用完全平方公式化简,得到关于m的方程,求出方程的解即可得到m的值.
解答 解:设直角三角形的两锐角分别为α,β,
根据题意得:方程4x2-2(m+1)x+m=0的两根为cosα与cosβ(sinα=cosβ),
∴cosα+cosβ=cosα+sinβ=-$\frac{-2(m+1)}{4}$,cosαsinβ=$\frac{m}{4}$>0,
又sin2α+cos2β=1,
∴(cosα+sinβ)2-2sinαcosβ=$\frac{(m+1)^{2}}{4}$-$\frac{m}{2}$=1,
整理得:m2=3,
解得:m=$\sqrt{3}$或m=-$\sqrt{3}$(舍去),
则m的值为$\sqrt{3}$.
点评 此题考查了一元二次方程根与系数的关系,以及互余两角三角函数的关系,熟练掌握根与系数的关系是解本题的关键.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:选择题
| A. | x≥-2且x≠2 | B. | x≥-2 | C. | x≠0 | D. | x<2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
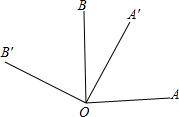 如图,把∠AOB绕点O逆时针旋转θ角,得到∠A′OB′.
如图,把∠AOB绕点O逆时针旋转θ角,得到∠A′OB′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com