Question

1．已知抛物线y=ax²-2ax+c与x轴交于A（-1，0）、B两点，交y轴于点C，E（-2，5）、F两点在抛物线上．
（1）求二次函数解析式；
（2）若△ACF的一个角的角平分线在坐标轴上，求点F的坐标；
（3）若△CEF的面积为5，直接写出点F的坐标．

Answer 1

分析 （1）利用待定系数法求二次函数的解析式；
（2）分两种情况讨论：①当y轴平分∠ACF时，如图2，当x轴平分∠FAC时，点F的坐标就是直线FC和抛物线的交点，②当x轴平分∠FAC时，如图3，直线AF与抛物线的交点；
（3）先设出点F的坐标，利用面积差列式计算．

解答 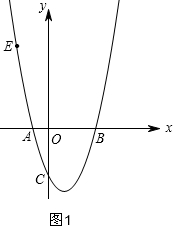解：（1）如图1，
把点A（-1，0）和点E（-2，5）分别代入函数解析式中得：
a+2a+c=0，4a+4a+c=5，
∴c=-3，a=1，
∴此二次函数的解析式为：y=x²-2x-3；
（2）当x=0时，y=-3，
∴C（0，-3），
分两种情况讨论：
①当y轴平分∠ACF时，如图2，
设CF与x轴交于点D，
∵A（-1，0），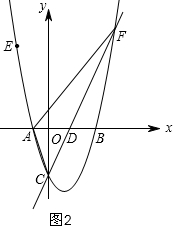
∴D（1，0），
设CF的解析式为：y=kx+b，
把C（0，-3）和D（1，0）代入得：$\left\{\begin{array}{l}{k+b=0}\\{b=-3}\end{array}\right.$，
解得$\left\{\begin{array}{l}{k=3}\\{b=-3}\end{array}\right.$，
∴CF的解析式为：y=3x-3，
则$\left\{\begin{array}{l}{y=3x-3}\\{y={x}^{2}-2x-3}\end{array}\right.$，
x²-2x-3=3x-3，
x₁=0（舍），x₂=5，
当x=5时，y=3×5-3=12，
∴F（5，12），
②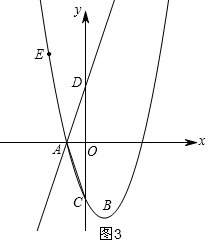当x轴平分∠FAC时，如图3，设直线AF交y轴于D，
同理得D（0，3），
此时AF的解析式为：y=3x+3，
则$\left\{\begin{array}{l}{y=3x+3}\\{y={x}^{2}-2x-3}\end{array}\right.$，
x²-2x-3=3x+3，
解得：x₁=6，x₂=-1（舍），
当x=6时，y=3×6+3=21，
∴F（6，21），
综上所述，符合条件的点F的坐标为（5，12）或（6，21）；
（3）设F（a，a²-2a-3），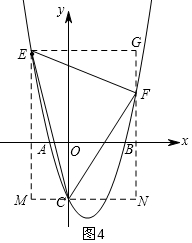
如图4，构建如图所示的矩形EMNG，
由题意得：S_△CEF=S_矩形EMNG-S_△EMC-S_△CNF-S_△EFG=5，
8（2+a）-$\frac{1}{2}$×2×8-$\frac{1}{2}$a（a²-2a-3+3）-$\frac{1}{2}$（a+2（5-a²+2a+3）=5，
解得：a=-1±$\sqrt{6}$，
当a=-1+$\sqrt{6}$时，a²-2a-3=（a-1）²-4=（-1$+\sqrt{6}$）²-4=6-4$\sqrt{6}$，
当a=-1-$\sqrt{6}$时，a²-2a-3=（-1-$\sqrt{6}$）²-4=6+4$\sqrt{6}$，
∴F（-1+$\sqrt{6}$，6-4$\sqrt{6}$）或（-1-$\sqrt{6}$，6+4$\sqrt{6}$）．

点评 本题是二次函数和一次函数的综合题，比较麻烦，考查了利用待定系数法求二次函数和一次函数的解析式；能准确求出抛物线与x轴交点（把y=0代入）和与y轴交点坐标（把x=0代入）；知道两函数图象的交点坐标就是两函数解析式所组成的方程组的解．