
【题目】若a,b,c是有理数,|a|=4,|b|=9,|c|=6,且ab<0,bc>0,求a﹣b﹣(﹣c)的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图所示的运算程序中,若开始输入的x值为12,我们发现第1次输出的结果为6,第2次输出的结果为3,…第2017次输出的结果为( ) 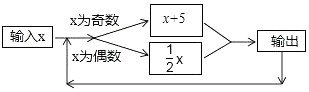
A.3
B.6
C.4
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式:
13+23= ![]() ×4×9=
×4×9= ![]() ×22×32
×22×32
13+23+33=36= ![]() ×9×16=
×9×16= ![]() ×32×42
×32×42
13+23+33+43=100= ![]() ×16×25=
×16×25= ![]() ×42×52
×42×52
(1)计算:13+23+33+43+…+103的值;
(2)猜想:13+23+33+43+…+n3的值.
(3)计算:513+523+533+…+993+1003的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个三角形的三边a,b,c能满足a2+b2=nc2(n为正整数),那么这个三角形叫做“n阶三角形”.如三边分别为1、2、![]() 的三角形满足12+22=1×(
的三角形满足12+22=1×(![]() )2,所以它是1阶三角形,但同时也满足(
)2,所以它是1阶三角形,但同时也满足(![]() )2+22=9×12,所以它也是9阶三角形.显然,等边三角形是2阶三角形,但2阶三角形不一定是等边三角形.
)2+22=9×12,所以它也是9阶三角形.显然,等边三角形是2阶三角形,但2阶三角形不一定是等边三角形.

(1)在我们熟知的三角形中,何种三角形一定是3阶三角形?
(2)若三边分别是a,b,c(a<b<c)的直角三角形是一个2阶三角形,求a:b:c.
(3)如图1,直角△ABC是2阶三角形,AC<BC<AB,三条中线BD、AE、CF所构成的三角形是何种三角形?四位同学作了猜想:
A同学:是2阶三角形但不是直角三角形;
B同学:是直角三角形但不是2阶三角形;
C同学:既是2阶三角形又是直角三角形;
D同学:既不是2阶三角形也不是直角三角形.
请你判断哪位同学猜想正确,并证明你的判断.
(4)如图2,矩形OACB中,O为坐标原点,A在y轴上,B在x轴上,C点坐标是(2,1),反比例函数y=![]() (k>0)的图象与直线AC、直线BC交于点E、D,若△ODE是5阶三角形,直接写出所有可能的k的值.
(k>0)的图象与直线AC、直线BC交于点E、D,若△ODE是5阶三角形,直接写出所有可能的k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型水果超市销售无锡水蜜桃,根据前段时间的销售经验,每天的售价x(元/箱)与销售量y(箱)有如表关系:
每箱售价x(元) | 68 | 67 | 66 | 65 | … | 40 |
每天销量y(箱) | 40 | 45 | 50 | 55 | … | 180 |
已知y与x之间的函数关系是一次函数.
(1)求y与x的函数解析式;
(2)水蜜桃的进价是40元/箱,若该超市每天销售水蜜桃盈利1600元,要使顾客获得实惠,每箱售价是多少元?
(3)七月份连续阴雨,销售量减少,超市决定采取降价销售,所以从7月17号开始水蜜桃销售价格在(2)的条件下,下降了m%,同时水蜜桃的进货成本下降了10%,销售量也因此比原来每天获得1600元盈利时上涨了2m%(m<100),7月份(按31天计算)降价销售后的水蜜桃销售总盈利比7月份降价销售前的销售总盈利少7120元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品厂向A市销售面包,如果从铁路托运,每千克需运费0.8元;如果从公路托运,每千克需运费0.5元,另需包装费 600元。
(1)设该市向A市销售面包![]() 千克,铁路运费
千克,铁路运费![]() 元,公路运费
元,公路运费![]() 元,则
元,则![]() 与
与![]() 之间的函数关系式分别为_______,_________;
之间的函数关系式分别为_______,_________;
(2)若厂家只出运费1500元,选用______ 运送,运送面包多;
(3)若厂家运送3000千克,选用______运送,所需运费少。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点A、B分别在数轴原点O的左右两侧,且 ![]() OA+50=OB,点B对应数是90.
OA+50=OB,点B对应数是90. ![]()
(1)求A点对应的数;
(2)如图2,动点M、N、P分别从原点O、A、B同时出发,其中M、N均向右运动,速度分别为2个单位长度/秒,7个单位长度/秒,点P向左运动,速度为8个单位长度/秒,设它们运动时间为t秒,问当t为何值时,点M、N之间的距离等于P、M之间的距离; ![]()
(3)如图3,将(2)中的三动点M、N、P的运动方向改为与原来相反的方向,其余条件不变,设Q为线段MN的中点,R为线段OP的中点,求22RQ﹣28RO﹣5PN的值. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(km)与行驶时间t(h)的函数图象如图所示,下列说法正确的有( )
①甲车的速度为50km/h
②乙车用了3h到达B城
③甲车出发4h时,乙车追上甲车
④乙车出发后经过1h或3h两车相距50km.

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
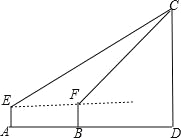
【题目】如图,一游客在某城市旅游期间,沿街步行前往著名的电视塔观光,他在A处望塔顶C的仰角为30°,继续前行250m后到达B处,此时望塔顶的仰角为45°.已知这位游客的眼睛到地面的距离约为170cm,假若游客所走路线直达电视塔底.请你计算这座电视塔大约有多高?(结果保留整数. ![]() ≈1.7,
≈1.7,![]() ≈1.4;E,F分别是两次测量时游客眼睛所在的位置.)
≈1.4;E,F分别是两次测量时游客眼睛所在的位置.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com